基本介紹
- 中文名:休克爾分子軌道法
- 外文名: Hückel molecular orbital method
- 簡稱:HMO
- 提出者:E.休克爾
原理
分類
薛丁格方程
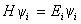
線性組合

久期方程
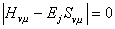
矩陣元

假定
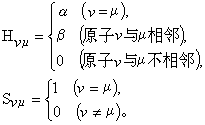
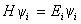

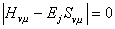

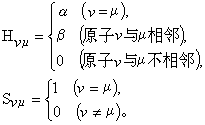
休克爾分子軌道法( Hückel molecular orbital method)是用簡化的近似分子軌道模型處理共軛分子中的π 電子的方法,1931年由E.休克爾(E. Hückel)提出,簡稱HMO。這...
簡介 休克爾分子軌道方法Hiickel molecular orbital method; HMO處理共扼體系中二電子的簡化的分子軌道方法。簡稱HM(7。該方法認為二電子是在原子實和。電子所形成...
推廣的休克爾分子軌道法是用簡化的近似分子軌道模型處理共軛分子中的π 電子的方法,1931年由E.休克爾(E. Hückel)提出,簡稱HMO。這是一種最簡單的分子軌道理論,...
休克爾方法(英語:Hückel method),又稱休克爾分子軌道法(英語:Hückel molecular orbital method,縮寫:HMO),是1930年埃里希·休克爾提出的一個計算分子軌道及能級...
休克爾(Erich Armand Arthur Joseph Hückel,1896年8月9日-1980年2月16日),...電解質溶液的德拜–休克爾理論 π電子體系分子軌道近似計算的休克爾方法 目錄...
套用微擾法討論分子軌道的理論。微擾法首先是由C.A.庫爾森和H.C.朗蓋特-希金斯引入到分子軌道理論中來的。在實際的化學問題中,常需要討論兩個緊密相關體系的差別...
為此,對照休克爾分子軌道法(HMO),在簡單自由電子模型中引進有效質量m*和新的能量零階U 作為可調參量,從分析相同芳香烴的光電子光譜π-帶位置得知,FEMO 不僅在...
30~40年代,L.C.鮑林提出的共振論、E.休克爾的分子軌道理論及雜化軌道理論等,推動了有機化學的發展,這是理論有機化學的開始階段。人們為了逐步運用量子化學計算...
菲的分子式也是C14H10,與蒽互為同分異構體,它也是由三個苯環稠合而成,但三個苯環不在一條直線上,其結構式為:休克爾規則1931年,休克爾從分子軌道理論角度提出...
鍵級又稱鍵序,是分子軌道法中表示相鄰的兩個原子成鍵強度的一種數值。對雙原子分子來說,把成鍵電子數與反鍵電子數的差值的一半,稱為鍵級。在形成共價鍵時,成...
第5章 多原子分子的結構和性質5.1多原子分子結構的一些原理和概念5.2雜化軌道理論5.3離域分子軌道理論5.4休克爾分子軌道法(HMO法)...
5.3 缺電子分子的結構小結習題科學家及其思想方法——鮑林的科學貢獻和研究方法6 共軛分子的結構6.1 休克爾分子軌道法(hmo)6.2 苯的離域辜*...
四、雙原子分子的結構和性質1 分子的電子組態與鍵級2 同核雙原子分子3 異核雙原子分子五、休克爾分子軌道法和共軛分子結構1 休克爾分子軌道法...
按照休克爾分子軌道法(HMO),每個π電子用一個π分子軌道來描寫,各個參與共軛的原子軌道的線性組合為:式中ni為第i個分子軌道上的π電子數,即占據數,各個qμ就...
第5章 多原子分子的結構與性質5.1 主要知識點5.1.1 價電子對互斥理論5.1.2 雜化軌道理論5.1.3 離域分子軌道理論5.1.4 休克爾分子軌道理論法(HMO法)...
在休克爾分子軌道法和推廣的休克爾分子軌道法中,集居數分析是簡單明了的,即直接計算出各原子上的電荷分布和鍵級就可以了。集居數分布表明了分子中電荷的分布,...
其本質是原子軌道重疊後,高機率地出現在兩個原子核之間的電子與兩個原子核之間...路易斯理論 價鍵理論 軌道雜化理論 互斥理論 分子軌道理論 分類 按成鍵方式 按...
第六節休克爾分子軌道法構造共軛分子 第七節共軛分子中離域π鍵的特徵量 第八節如何構造簡單的多原子分子 第四章分子的對稱性 第一節分子對稱性的概念 ...
實驗25 休克爾分子軌道法實驗26 徑向分布函式、角度分布函式與電子云圖形的繪製實驗27 電子躍遷參數的測定實驗28 紅外吸收光譜與分子振動運動Ⅲ 提高型實驗(綜合性、...
第5章 多原子分子中的化學鍵5.1 價電子對互斥理論5.2 雜化軌道理論5.3 離域分子軌道理論5.4 休克爾分子軌道法5.5 離域健和共軛效應...
