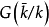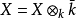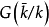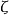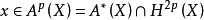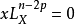基本介紹
- 中文名:代數閉鏈
- 外文名:algebraic cycle
- 性質:概念
- 學科:數學
- 提出者:龐加萊
簡介,性質,
簡介
代數閉鏈是代數簇上的由給定代數簇的所有不可約子簇作為自由生成元集合的自由阿貝尓群(free Abelian group) 的一個元素。簇 X 上的代數閉鏈的群記為 ,
, 中由余維數為 p 的子簇生成的子群記為
中由余維數為 p 的子簇生成的子群記為 。群
。群 可以表示成直和
可以表示成直和




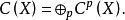
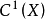
性質
設 X 表示代數閉域 k 上 n 維奇異射影代數簇。若 k 是複數域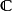 ,則每個代數閉鏈
,則每個代數閉鏈 定義了一個
定義了一個 維同謂類
維同謂類 ,且根據龐加萊對偶性,確定一個上同調類
,且根據龐加萊對偶性,確定一個上同調類 (或
(或 )型的同調(或上同調)類稱為代數同謂(或上同調)類。每個解析閉鏈都同謂於一個代數閉鏈。人們相信(霍奇猜想)X 上的一個整
)型的同調(或上同調)類稱為代數同謂(或上同調)類。每個解析閉鏈都同謂於一個代數閉鏈。人們相信(霍奇猜想)X 上的一個整 維閉鏈
維閉鏈 同謂於一個代數閉鏈,若且唯若所有
同謂於一個代數閉鏈,若且唯若所有 型閉微分形式在
型閉微分形式在 的積分等於 0。這個猜想只是對
的積分等於 0。這個猜想只是對 ,對
,對 以及對簇的一些孤立類得到證明。
以及對簇的一些孤立類得到證明。
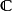











如果 是兩個簇的積
是兩個簇的積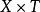 上的一個代數閉鏈,則 X 上形如
上的一個代數閉鏈,則 X 上形如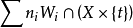 的閉鏈的集合稱為 X 上以基數 T 參量化的代數閉鏈族(family of algebraic cycles)。
的閉鏈的集合稱為 X 上以基數 T 參量化的代數閉鏈族(family of algebraic cycles)。

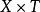
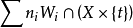
這種關係通常要求每個子簇 到 T 上的射影是平坦態射。當
到 T 上的射影是平坦態射。當 由不可約子簇定義時,X 上相應的代數閉鏈族稱為代數子簇族(family of algebraic subvarieties)。特別地,對代數簇的任何平坦態射
由不可約子簇定義時,X 上相應的代數閉鏈族稱為代數子簇族(family of algebraic subvarieties)。特別地,對代數簇的任何平坦態射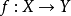 ,它的纖維
,它的纖維 構成一個以基簇 Y 參量化的 X 代數子簇族。這個概念的第二個特例是線性系。以連通基簇參量化的射影簇 X 的代數子簇(或相應地,代數閉鏈)族的所有成員都有相同的希爾伯特多項式(相應地,算術虧格)。
構成一個以基簇 Y 參量化的 X 代數子簇族。這個概念的第二個特例是線性系。以連通基簇參量化的射影簇 X 的代數子簇(或相應地,代數閉鏈)族的所有成員都有相同的希爾伯特多項式(相應地,算術虧格)。


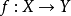

稱簇 X 上的兩個代數閉鏈  和
和 是代數等價的 (algebraically equivalent)(記為
是代數等價的 (algebraically equivalent)(記為 )。若
)。若 ,
,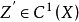 時,有理等價性的概念就簡化為除子的線性等價性的概念。有理(或相應地,代數)等價於零的代數閉鏈的子群記為
時,有理等價性的概念就簡化為除子的線性等價性的概念。有理(或相應地,代數)等價於零的代數閉鏈的子群記為 (相應地,
(相應地, )。這兩個群都是它的分量的直和:
)。這兩個群都是它的分量的直和:




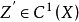








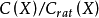
對任何韋伊上同調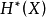 ,存在唯一確定的群同態
,存在唯一確定的群同態 ,如果
,如果 ,就稱兩個代數閉鏈
,就稱兩個代數閉鏈 和
和 是同調等價的 (homologically equivalent)(記為
是同調等價的 (homologically equivalent)(記為 )。同調等價於 0 的代數閉鏈的子群記為
)。同調等價於 0 的代數閉鏈的子群記為 。存在嵌入
。存在嵌入 。商群
。商群 是有限生成的,而且是環
是有限生成的,而且是環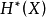 的子環,記為
的子環,記為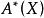 ,稱作代數韋伊上同調類的環(ring of algebraic Weil cohomology classes)。還不知道
,稱作代數韋伊上同調類的環(ring of algebraic Weil cohomology classes)。還不知道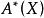 是否依賴於選取的韋伊上同調論。
是否依賴於選取的韋伊上同調論。
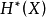








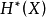
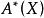
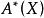
如果存在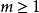 使
使 ,就稱兩個代數閉鏈
,就稱兩個代數閉鏈 和
和 是
是  等價的(r-equivalent)(記為
等價的(r-equivalent)(記為  )。
)。 等價於 0 的代數閉鏈的子群記為
等價於 0 的代數閉鏈的子群記為 。
。 的兩個代數閉鏈
的兩個代數閉鏈 和
和 稱為數值等價的 (numerically equivalent)(記為
稱為數值等價的 (numerically equivalent)(記為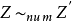 ),如果對任何
),如果對任何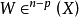 ,只要等式兩邊都有定義,就有
,只要等式兩邊都有定義,就有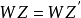 。數值等價於 0 的代數閉鏈的子群記為
。數值等價於 0 的代數閉鏈的子群記為 。有如下嵌入:
。有如下嵌入:
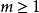










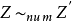
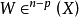
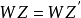


對於除子,群 ,
, 和
和 是相同的。不過有如下反例:對於
是相同的。不過有如下反例:對於 ,這裡的
,這裡的 是作為有理係數的尋常上同調的 l 進理論,可舉出類似的反例。關於群
是作為有理係數的尋常上同調的 l 進理論,可舉出類似的反例。關於群 與
與 的相等問題以及解決。
的相等問題以及解決。







在這種情形下,如果 k 是複數域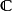 ,則雙線性型
,則雙線性型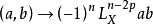 在
在 中本原類的子空間上是正定的。對於任意 k,類似命題僅對一些特殊情形得到證明,它與代數簇
中本原類的子空間上是正定的。對於任意 k,類似命題僅對一些特殊情形得到證明,它與代數簇 函式上的韋伊猜想密切相關。
函式上的韋伊猜想密切相關。
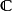
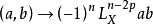


當簇 X 定義在非代數閉域 k 上時,域 k 的可分代數閉包的伽羅瓦群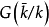 作用在韋伊上同調
作用在韋伊上同調 上,這裡
上,這裡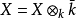 的每個元素關於群
的每個元素關於群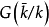 的有限指數的某子群保持不變。人們相信(代數閉鏈的泰特猜想( Tate conjecture on algebraic cycles))如果 k 在它的素子域上有限生成,則其逆命題也正確。代數簇
的有限指數的某子群保持不變。人們相信(代數閉鏈的泰特猜想( Tate conjecture on algebraic cycles))如果 k 在它的素子域上有限生成,則其逆命題也正確。代數簇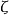 函式上的許多猜想都以這個假設為基礎。
函式上的許多猜想都以這個假設為基礎。