人工耗散是指在數值求解雙曲型方程時,人為地或由於格式自動地引入擴散項,起黏性耗散作用,產生平滑效果。
對於一個不含這些項的偏微分方程,耗散項可能由於區域與方程的離散化而引人差分格式,它使得數值解的每個傅立葉分量振幅隨時間衰減,是差分格式的穩定因素。在合理取值情況下,小的可壓縮係數對疊代有利和人工耗散有助於數值收斂。
基本介紹
- 中文名:人工耗散
- 外文名:artificial dissipation
- 套用:數值求解
- 特點:人為地或格式自動地引入擴散項
- 作用:起黏性耗散作用,產生平滑效果
- 學科:空氣動力學
定義,雙曲型方程,耗散項,簡介,人工耗散對數值計算的影響,
定義
人工耗散是指在數值求解雙曲型方程時,人為地或由於格式自動地引入擴散項,起黏性耗散作用,產生平滑效果。
雙曲型方程
雙曲型偏微分方程(Hyperbolic partial differential equations):描述振動或波動現象的偏微分方程。它的一個典型特例是波動方程和n=1時的波動方程。可用來描述弦的微小橫振動,稱為弦振動方程。這是最早得到系統研究的一個偏微分方程。
如果一個微分方程中出現的未知函式只含一個自變數,這個方程叫做常微分方程,也簡稱微分方程;如果一個微分方程中出現多元函式的偏導數,或者說如果未知函式和幾個變數有關,而且方程中出現未知函式對幾個變數的導數,那么這種微分方程就是偏微分方程。
耗散項
耗散項(dissipative term)是偏微分方程數值解法術語,指微分方程或差分格式中,表達相當於粘性、熱傳導與擴散等使機械能耗散的項。對於一個不含這些項的偏微分方程,耗散項可能由於區域與方程的離散化而引人差分格式,它使得數值解的每個傅立葉分量振幅隨時間衰減,是差分格式的穩定因素。
簡介
在氣動聲學(CAA)計算中,滿足色散關係是CAA數值格式設計中最為重要的內容。由於任何格式的色散關係只能在低波數(長波)範圍保持,而在高波數(短波)範圍內會引起誤差,且色散誤差隨時間和距離的延長而增加,因此數值計算得到的波形嚴重失真。Tam等人為了克服這個困難,在由DRP ( Dispersive Relation Preserving)格式離散的差分方程上加一人工選擇耗散項(七點形式),使得短波被去除,而長波卻沒有影響。
南昌陸軍學院的王澤暉通過算例研究了人工選擇耗散法消除“偽“數值振盪的能力有捕獲激波能力,良好的計算結果表明該方法具套用線上性與非線性氣動聲學問題中是可行的,同時也說明除了DRP格式,人工選擇耗散也能與其它一些常用的數值格式(對稱格線點)相結合。他提出了建立非對稱格線的人工選擇耗散法。並把人工選擇耗散法套用於二維問題。數值結果證明該方法具有良好的消除振盪能力,不僅能用於氣動聲學計算,也可以用於一般的數值計算。
人工耗散對數值計算的影響
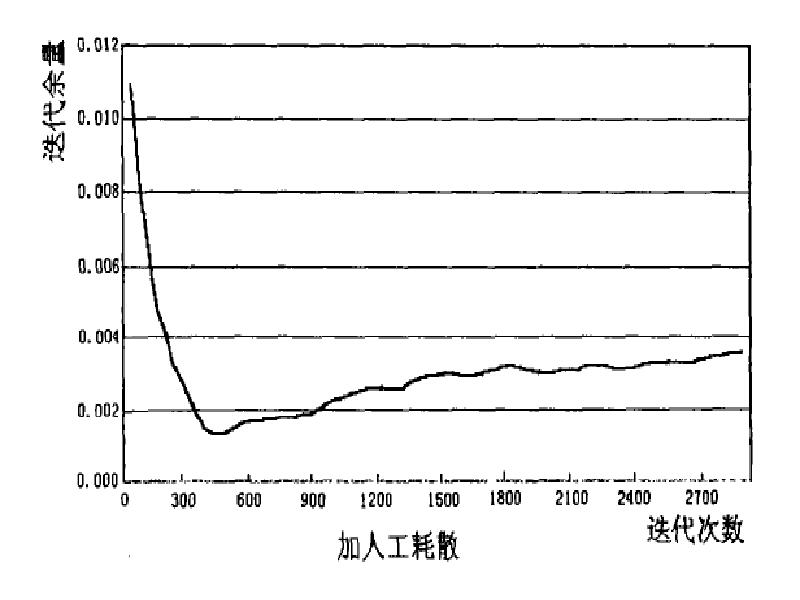
為了衡量人工耗散在數值計算中的作用,在其他條件(後台階繞流,Re=80)相同情況下,採用無人工耗散和顯式添加四階人工耗散兩種方法進行計算,連續性方程疊代餘量的變化曲線如圖(a)(b)。從圖可以看出,在疊代時添加人工耗散不僅有助於解的收斂,而且對消除疊代過程中解的振盪很有幫助。
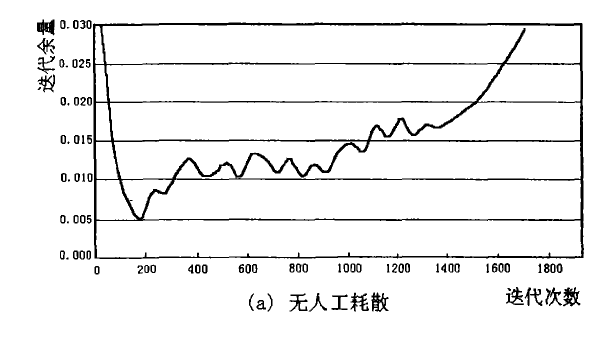
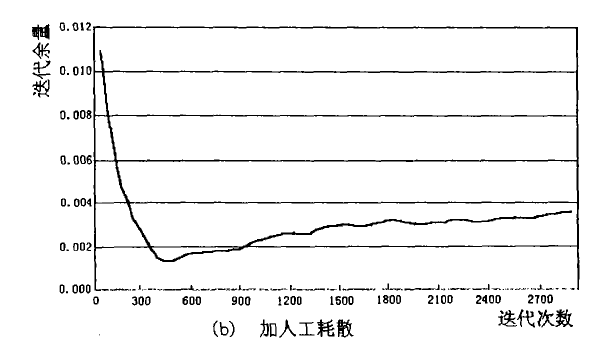
可以看出,在合理取值情況下,小的可壓縮係數對疊代有利和人工耗散有助於數值收斂。