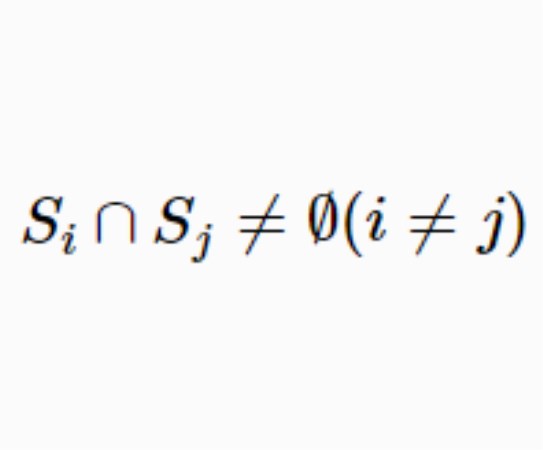基本介紹
- 中文名:交鄰圖
- 外文名:intersection graph
- 所屬學科:數學
- 所屬問題:組合學(圖與超圖)
- 簡介:由一個子集族產生的圖
- 舉例:區間圖、邊圖、團圖等
基本介紹,舉例說明,
基本介紹
交鄰圖是由一個子集族產生的圖。設F={S1,S2,…,Sp}是由一個有限集S的p個不同的非空子集S1,S2,…,Sp組成的族,以F為節點集,節點Si和Sj有邊相連當Si∩Sj≠∅(i≠j),這樣所得的圖稱為F的交鄰圖,常記為Ω(F)。
舉例說明
下面所列的圖中,區間圖、邊圖、團圖、塊圖、盒圖、圓圖和樹路圖均是交鄰圖;但是,割點圖、塊-割點圖和冪圖皆非交鄰圖。
以數軸上的一些區間作為節點,兩節點有一條邊相連若且唯若它們所對應的區間的交非空,這樣所得的圖稱為區間圖,區間圖還有兩種有意義的推廣,一種叫盒圖:節點集為n維立方體的集合,兩節點相鄰若且唯若它們對應的兩個立方體相交,另一種叫樹路圖:節點集為一樹上的一些路組成的集合,兩節點相鄰若且唯若它們對應的兩條路有公共部分(包括有公共端點)。若將節點代表平面上一個圓的不包括二端點的弦,兩節點相鄰若且唯若它們相應的弦有一個公共點,稱這樣的圖為圓圖。
一個圖G的邊圖是指由G這樣得到的圖:節點集為G的邊集,兩節點有一條邊相連若且唯若它們所對應的邊在G中相鄰,常用L(G)表示G的邊圖,圖L(G)的邊圖稱為G的2疊邊圖,常記為L2(G)。類似地,G的k疊邊圖就是指G的(k-1)疊邊圖的邊圖,常記為Lk(G)。
一個圖G的團圖是指這樣的圖:以G的每個團作為節點,兩節點有一條邊相連若且唯若它們所對應的團有公共節點,G的團圖常記為cl(G),cl(G)也稱為G的1疊團圖,G的(k-1)疊團圖的團圖稱為G的k疊團圖,常記為clk(G),k≥2。
一個圖G的塊圖是指這樣的圖:以G的每個塊作為節點,兩節點有一條邊相連若且唯若它們所對應的塊有公共節點,G的塊圖常記為B(G),一個圖G的割點圖是指這樣的圖;以G的每一個割點作為節點,兩節點有一條邊相連若且唯若它們所對應的割點在同一塊中,G的割點圖常記為C(G)。
一個圖G的塊-割點圖是指這樣的圖:以G的所有塊和所有割點組成的集合為節點集,兩節點有一條邊相連,若且唯若它們對應於一個塊和一個割點,並且這個塊含這個割點,G的塊-割點圖常記為BC(G)。
一個圖G的k冪圖(k≥1)是指這樣的圖:以G的節點集為節點集,兩節點有一條邊相連,若且唯若它們對應於G的節點在G上的距離最多為k,G的k冪圖常記為Gk,當然,G的1冪圖就是G本身。