基本介紹
適用定律
似穩電路
條件和集中參量







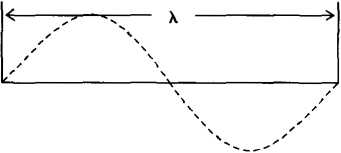
正弦式交流電











純電路
規律 | 純電阻電路 | 純電感電路 | 純電容電路 |
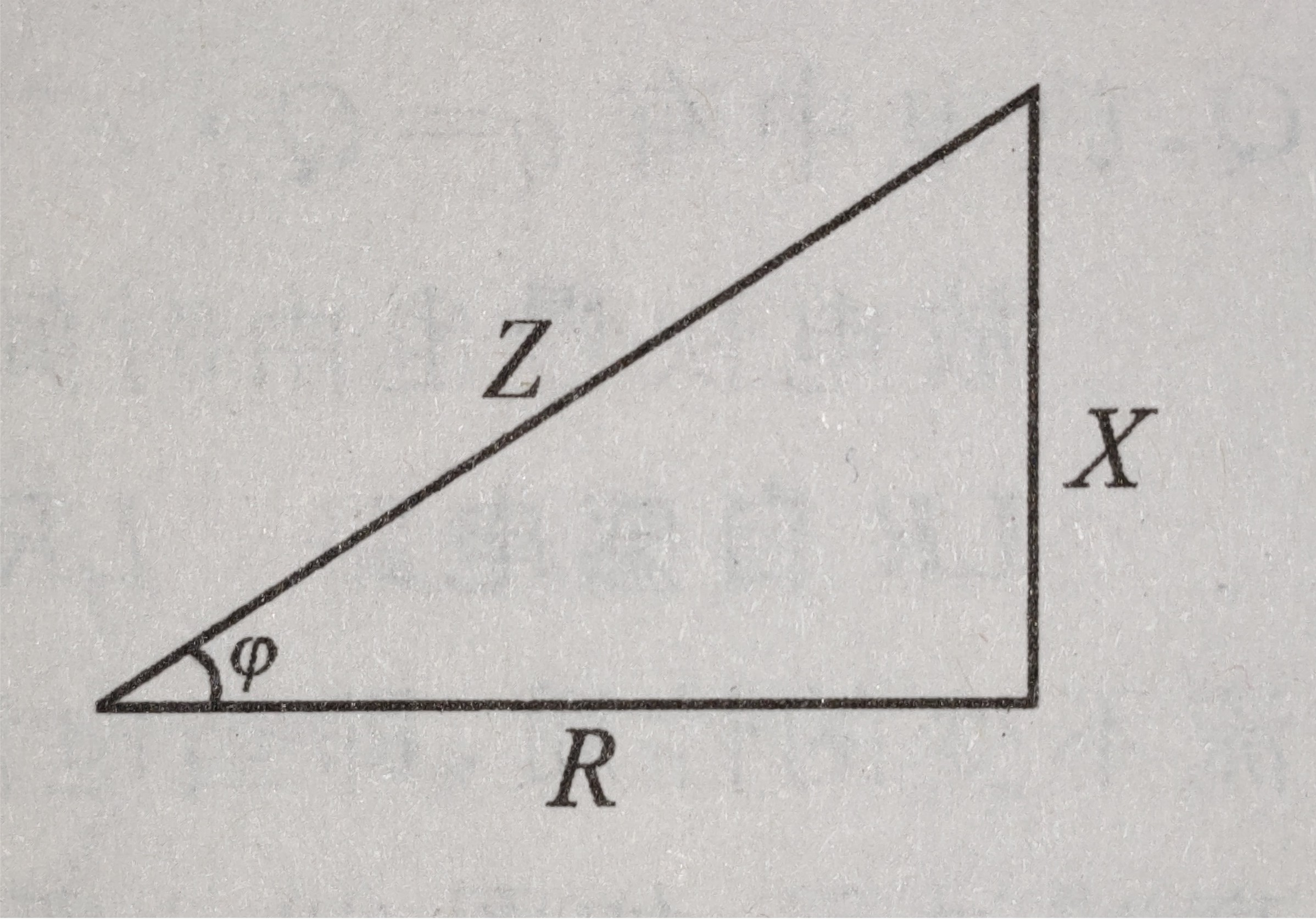
阻抗 |  |  |  |
歐姆定律形式 |  |  |  |
電壓電流變化相位關係 | 同相 | 電壓超前電流  | 電流超前電壓  |
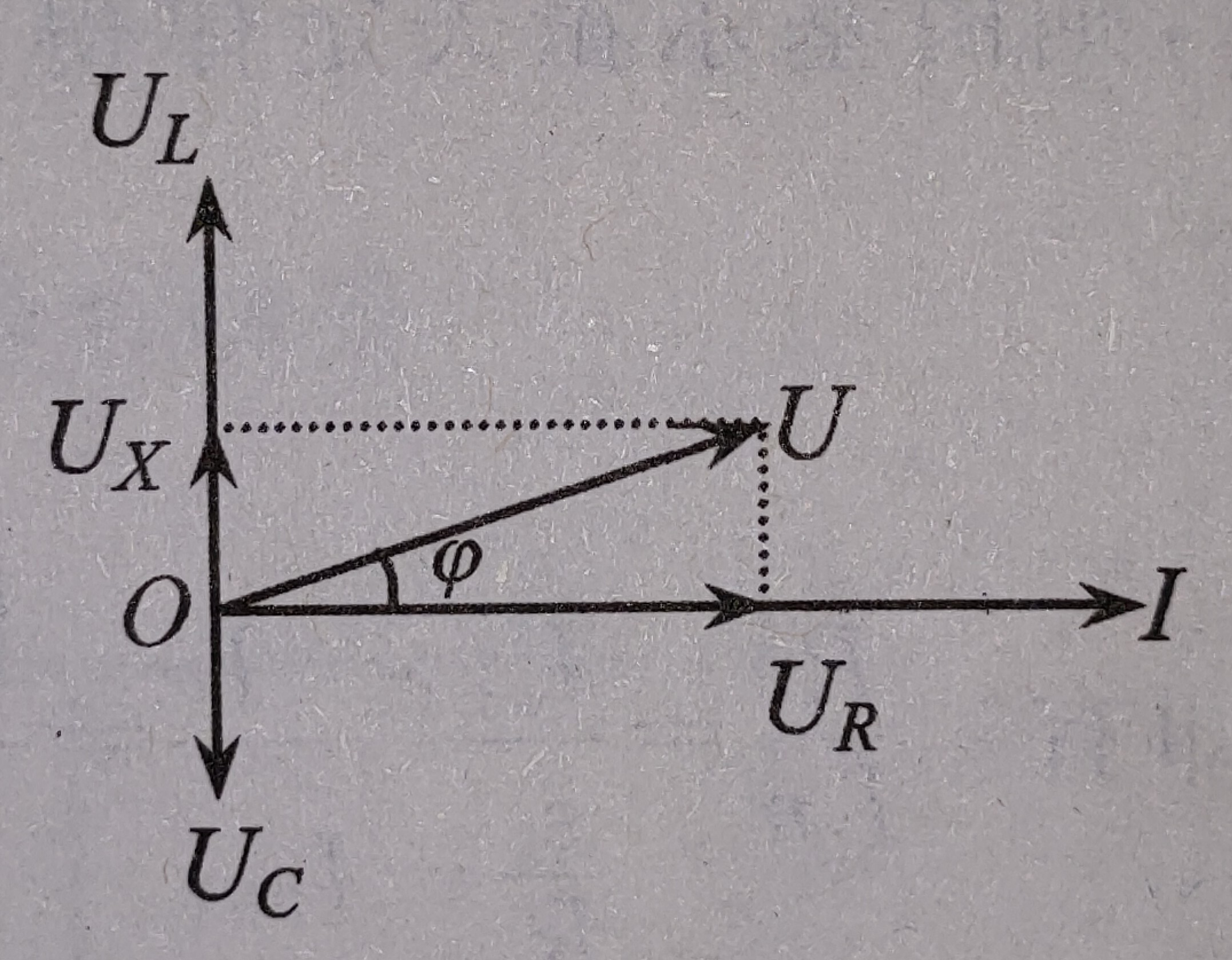
矢量圖 | 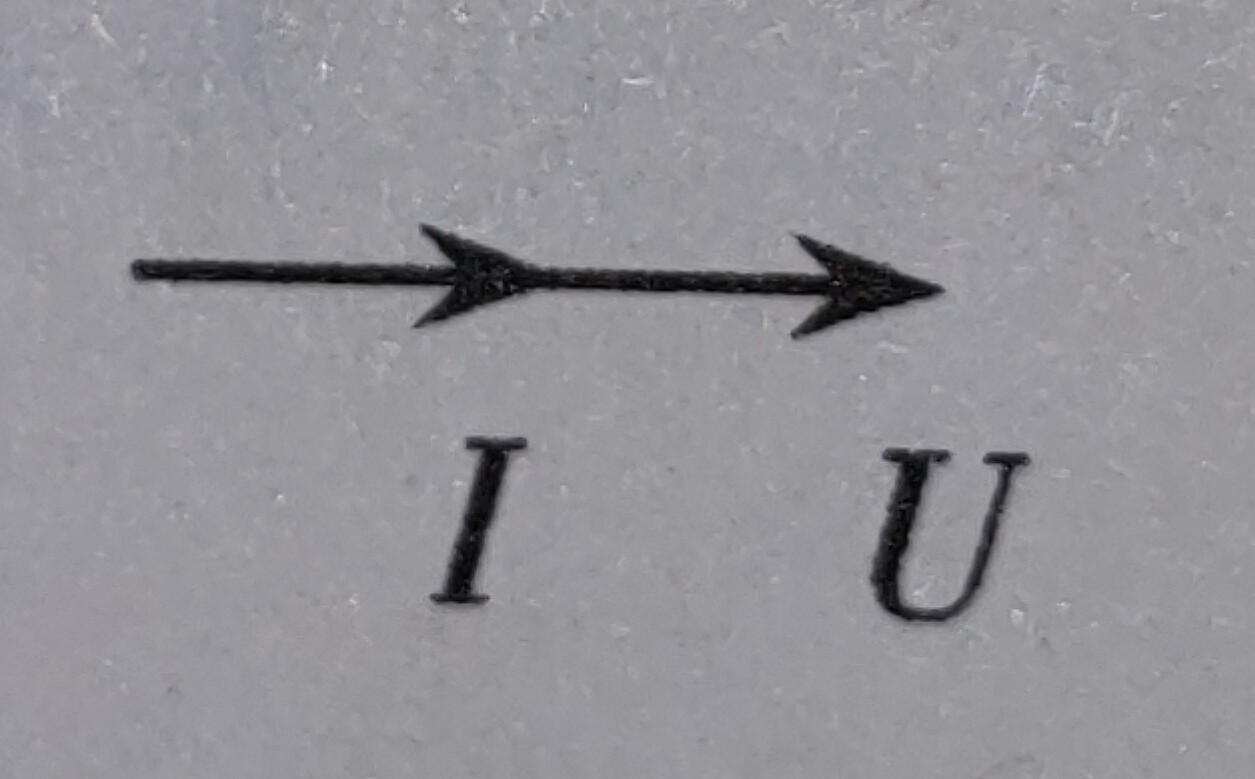 純電阻電路 | 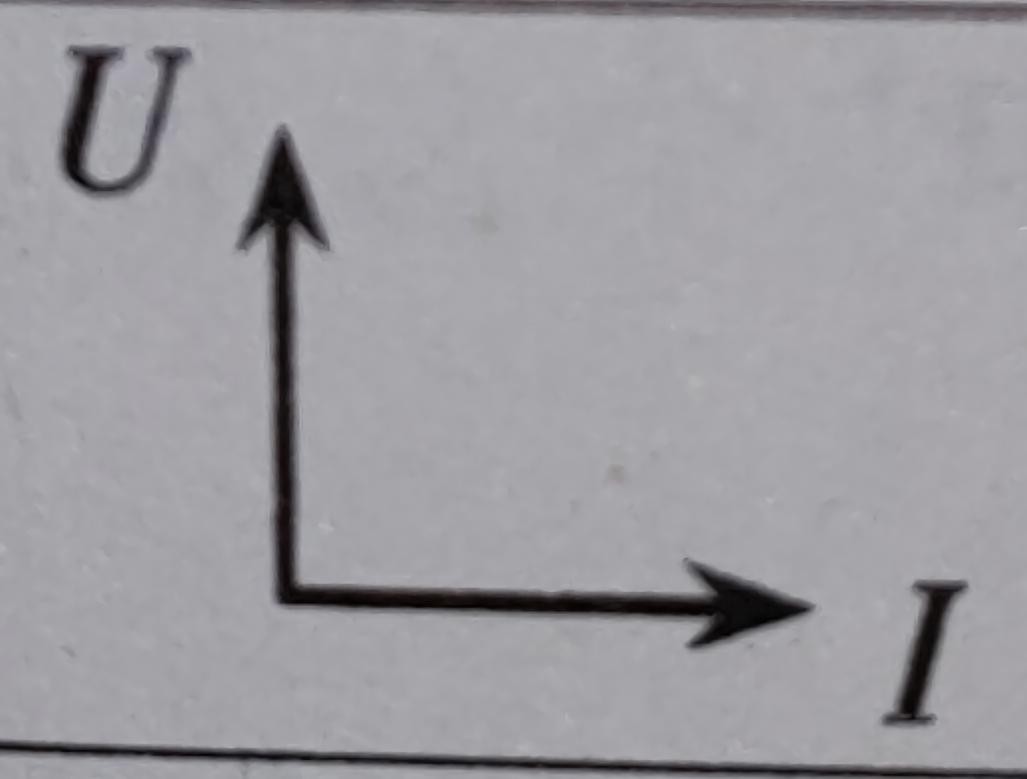 純電感電路 | 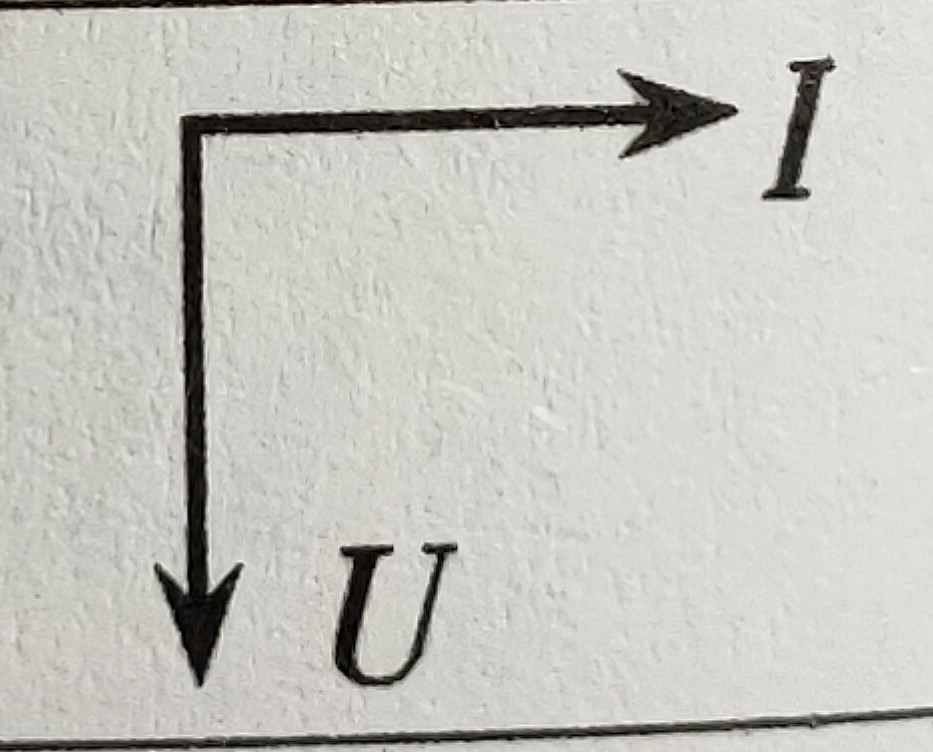 純電容電路 |
能量 | 消耗電能  | 存儲磁場能  | 存儲電場能  |
簡單串聯電路

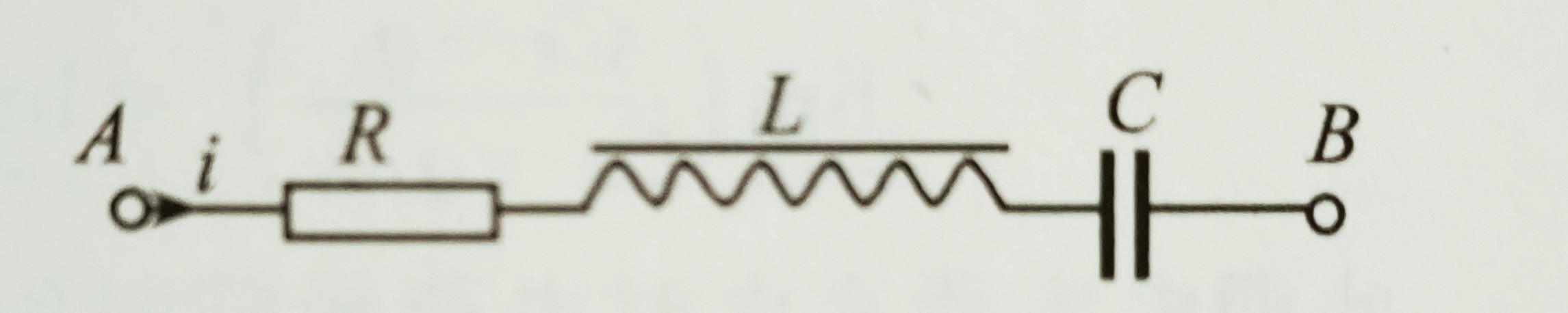
















暫態過程




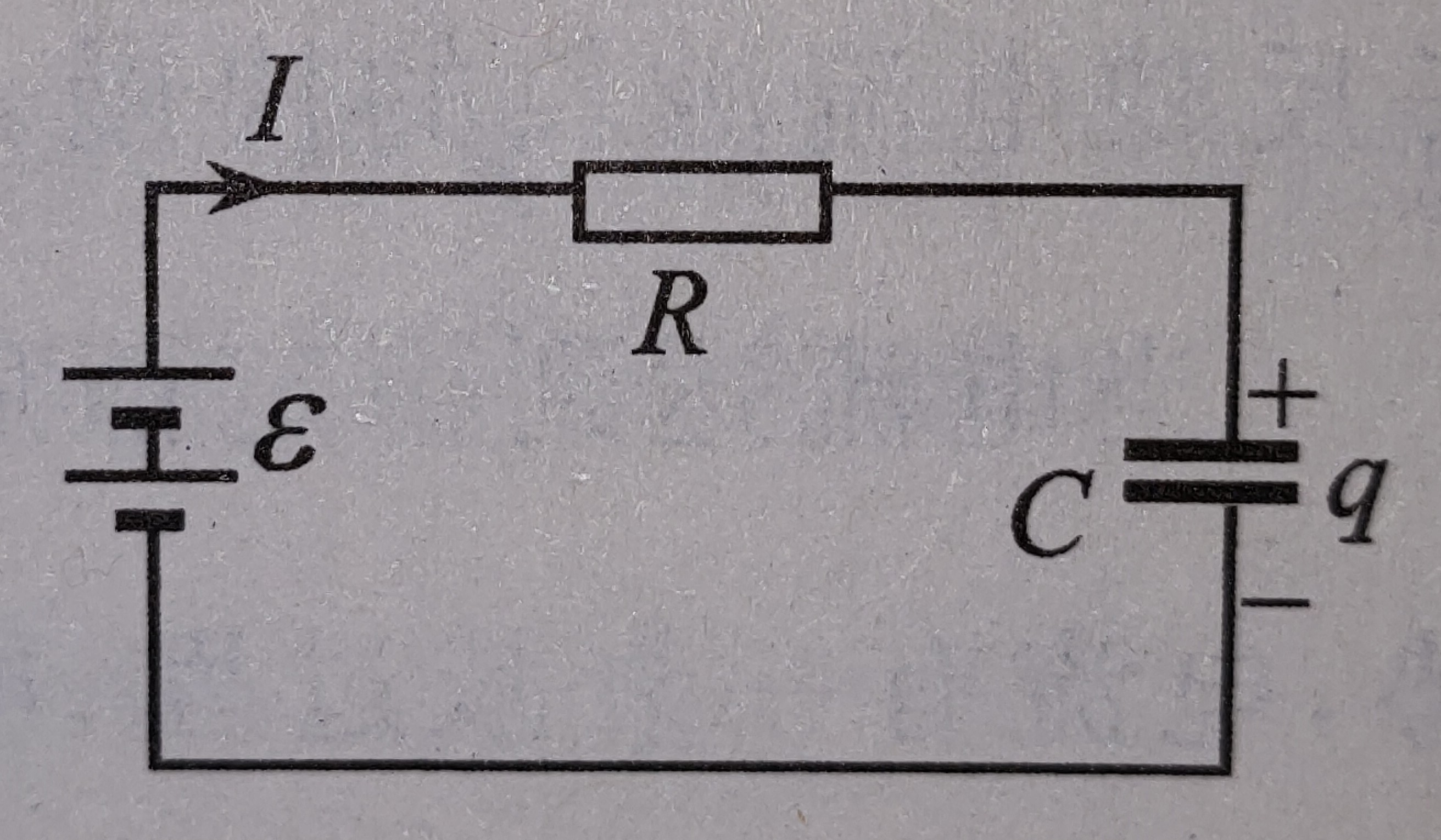



















規律 | 純電阻電路 | 純電感電路 | 純電容電路 |
阻抗 |  |  |  |
歐姆定律形式 |  |  |  |
電壓電流變化相位關係 | 同相 | 電壓超前電流  | 電流超前電壓  |
矢量圖 | 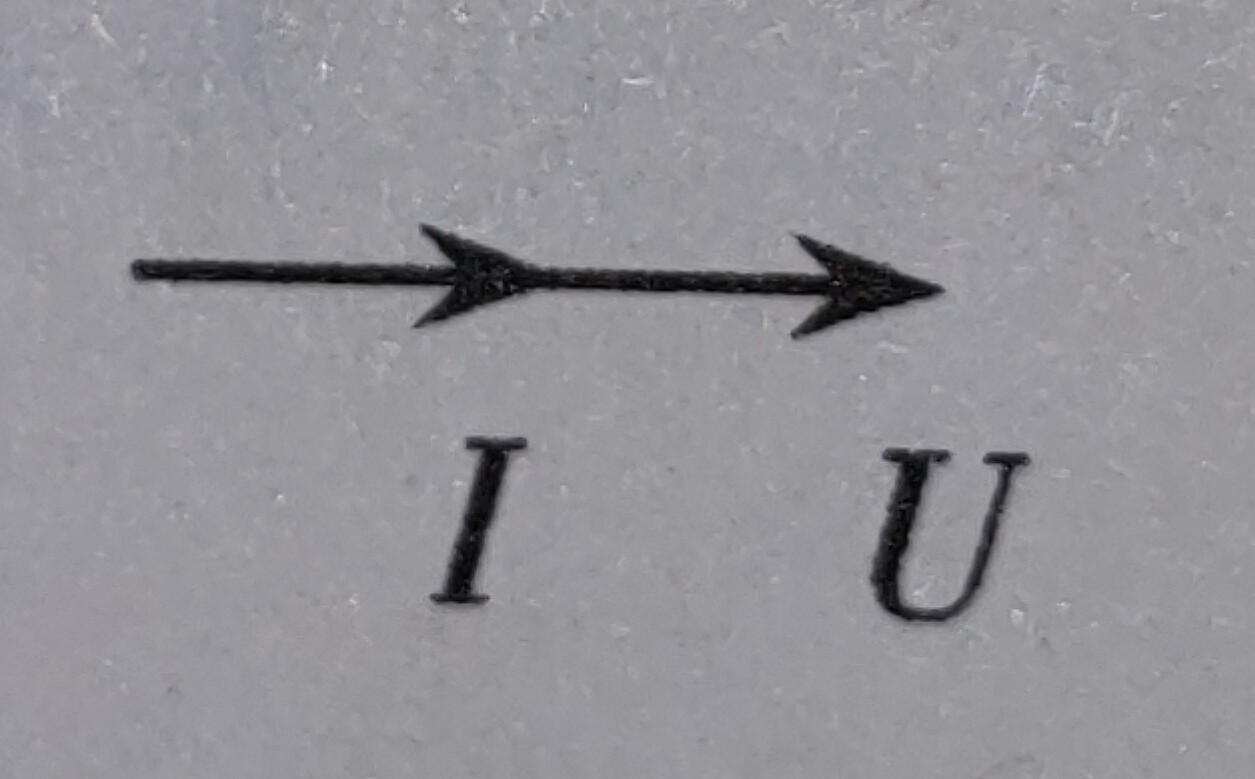 純電阻電路 |  純電感電路 |  純電容電路 |
能量 | 消耗電能  | 存儲磁場能  | 存儲電場能  |

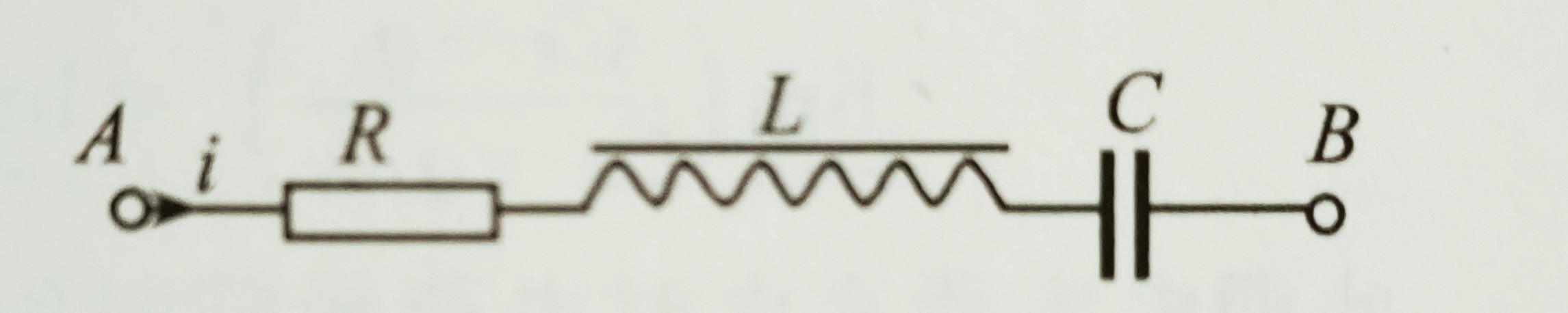























生產和生活中經常接觸電路,根據電路的情況可將電路分為穩恆電路和交變電路。若電源電動勢e隨時間作周期性變化,則各段電路中的電荷分布p、電壓u和電流I也隨時間作周期性變化,這種電路叫交變電路。適用定律交變電路也同時伴隨交變電...
交-交變流電路即把一種形式的交流電變成另一種形式的交流電的電路,在進行交-交變流時,可以改變相關的電壓、電流、頻率和相數等;其主要有;交流調壓電路,交流調功電路,交流電力電子開關,交交變頻電路等幾種電路形式。
這種按正弦規律變化的交變電流叫做正弦式交變電流,簡稱正弦式電流(sinusoidal current).正弦式電流是最簡單最基本的交變電流.電力系統中套用的大多是正弦式電流.正弦式電流的有效值 I U 與峰值 Im Um 之間有如下關係 I=Im/(根號2...
正弦交流電是隨時間按照正弦函式規律變化的電壓和電流。由於交流電的大小和方向都是隨時間不斷變化的,也就是說,每一瞬間電壓(電動勢)和電流的數值都不相同,所以在分析和計算交流電路時,必須標明它的正方向。術語簡介 隨時間作正弦...
大小和方向都做周期性迅速變化的電流,叫做振盪電流。是一種頻率很高的交變電流,在振盪電路中產生。定義 振盪電流是一種交變電流,是一種頻率很高的交變電流,它無法用線圈在磁場中轉動產生,只能是由振盪電路產生。能產生振盪電流的...
在原線圈上加交變電壓U₁,原線圈中就有交流電通過,在鐵芯中產生交變的磁通量。這個交變的磁通量也穿過副線圈,在副線圈中引起感應電動勢。所以,這時的副線圈可以作為電源使用。當把用電器連線在副線圈的兩端時,副線圈電路中就...
正弦電流是最簡單又最基本的交變電流。電力系統中套用的大多是正弦電流。在電子技術中也常遇到其他形式的交變電流。ω=2 f f 是頻率,單位Hz。得出頻率可知周期T,T=1/f 非正弦電流 不按正弦規律隨時間變化的交變電流叫非正弦...
振盪器就是可以產生一定頻率的交變電流信號的電路.晶體振盪器,以下簡稱晶振,是利用了晶體的壓電效應製造的,當在晶片的兩面上加交變電壓時,晶片會反覆的機械變形而產生振動,而這種機械振動又會反過來產生交變電壓。當外加交變電壓的...
