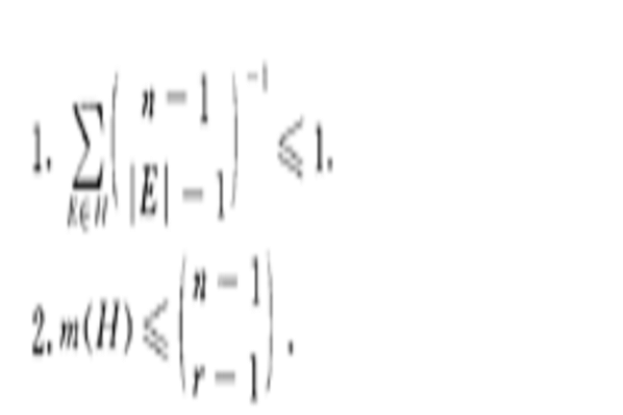交族(intersecting family)邊的集合。給定一個超圖H,稱它的邊的一個集合為交族,其中任意兩條邊的交均非空。若H本身就是一個交族,則超圖H稱為交超圖。
基本介紹
- 中文名:交族
- 外文名:intersecting family
- 分類:集合
- 屬性:數學術語
- 相關:交超圖
簡介,集族,相關研究,
簡介
愛爾特希一柯一拉多定理:若H是一個階為n的簡單超圖,H的秩r(H)=ran/2,H的度記為m(H),則更進一步,當H是K(r<n/2)的一個時,等式成立。這一定理首次在愛爾特希(Erdos,P.)、柯召和拉多(Rado,R.)於1961年聯名發表的一篇文章中。
集族
集族是一種特殊的集合,以集合為元素的集合稱為集族。例如,集A的冪集P(A)是一個集族,P(P(A)),P(P(P(A))都是集族。又例如,由空集φ、集合A={1,2,3}作為元素的集合M={φ,A}是一個集族。 注意,由空集φ作為元素的集合是一個集族,它已不是空集,即A={φ},它不同於{ }。
在這裡,A= {φ}是具有一個元素的集合,是單元素集。集族常用花體字母A,B,C等表示,取A為標號集,A到集族A的一一對應(雙射)為f:a→Aa,則集族A可記為{Aa|a∈A}或{Aa}a∈A。當A為線性序集{…,a,…,b,…,c,…}時,集族{…,Aa,…,Ab,…,Ac,…}稱為集列。
集族(family of sets)是由具有某種性質的一些集合所構成的集合,即“集合的集合”。例如,平面上的圓盤是集合,因此平面上一切圓盤所成的集合就是一個集族。又如一個集合的一切子集所構成的集合也是一個集族。
相關研究
有限集交族是組合數學的一個重要分支,研究的是[n]={1,2,…,n}的子集族在滿足特定性質下,其元素個數的上界問題。對有限集交族的研究方法主要有關聯矩陣法,幾何半格法,多重線性多項式的線性無關性方法。