內容,證明,
內容
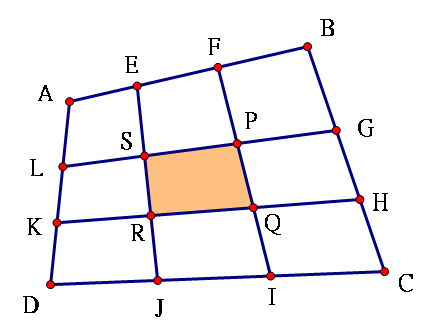
已知:一凸四邊形ABCD,E,F,G,H,I,J,K,L分別為其四邊上的三等分點
求證:四邊形PQRS的面積為四邊形ABCD面積的1/9
證明
張景中院士一本《新概念幾何》中給出了證明,但是用到到了定比分點公式(不是解析幾何那個),這裡將證明簡化一下: 證明分兩步,如下:
第一步:證明四邊形LKHG面積為四邊形ABCD面積的1/3
連線BL,BD,HL,HD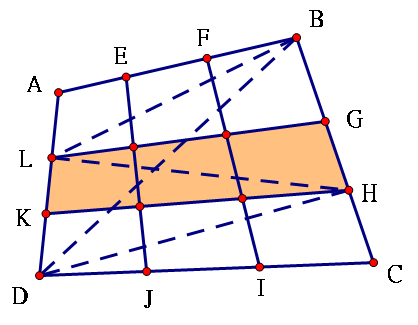

∵AL=LK=KD=1/3AD
∴LD=2/3AD
∴S△BDL=2/3*S△ABD ……(1)
同理S△BDH=2/3*S△BCD ……(2)
(1)+(2)得:
四邊形BLDH面積=S△BDL+S△BDH
=2/3*S△ABD +2/3*S△BCD
=2/3(△ABD +S△BCD)
=2/3四邊形ABCD面積
∵LK=KD=1/2LD
∴S△LKH=1/2*S△LDH
同理S△LGH=1/2*S△BLH
∴四邊形LKHG面積=S△LKH+S△LGH
=1/2*S△LDH+1/2*S△BLH
=1/2*四邊形BLDH面積
=1/2*2/3*四邊形ABCD面積
=1/3四邊形ABCD面積
第二步:證P,R,Q,S是GL,HK的三等分點
由三等分點知:BF=1/3AB,BG=1/3BC
∴FG∥AC,FG=1/3AC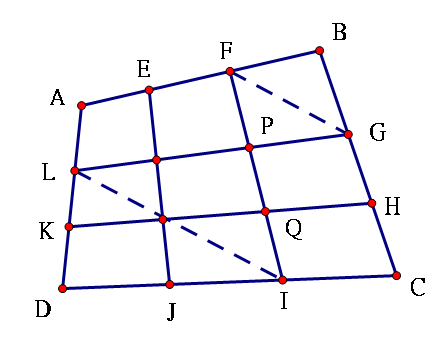

同理LI∥ACLI=2/3AC
所以FG∥LI,FG=1/2LI
∴△ILP∽△FGP=>PI=2FP,PL=2PG
∴P為GL三等分點
同理可證Q,R,S為三等分點
所以四邊形PQRS面積=1/3*四邊形GHLK面積=1/9四邊形ABCD面積
證畢。

