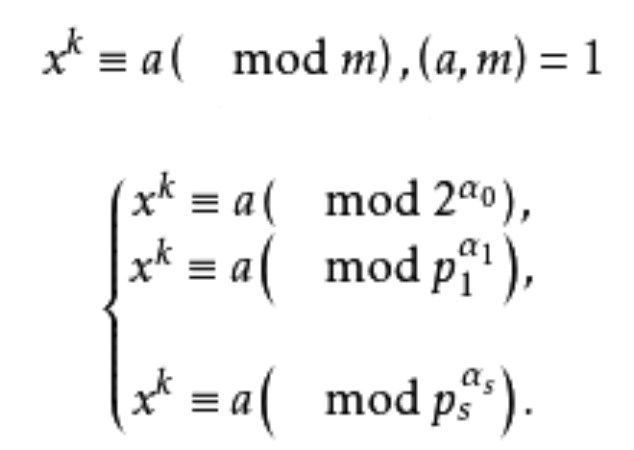二項同餘方程(binomial congruence equation)亦稱二項同餘式，是一類特殊的同餘方程，設k≥1，同餘方程x≡a(mod m)，(a，m)=1被稱為是模m的二項同餘方程。
基本介紹
- 中文名：二項同餘方程
- 外文名：binomial congruence equation
- 所屬學科：數學
- 所屬問題：初等數論(原根和指數)
- 別名：二項同餘式
- 簡介：一類特殊的同餘方程
基本介紹,二項同餘方程的解,
基本介紹
設整數k≥1，正整數m的標準分解式為
，而形如
利用原根的最小指數表可以解出(2)中的每一個同餘方程。若(1)有解，則稱a為模m的k次剩餘；若(1)無解，則稱a為模m的k次非剩餘。a是模m的k次剩餘的充分必要條件是a為每一個模
(i=1，2，…，s)的k次剩餘，因此，(1)若有解，則根據孫子定理可歸結為解形如
二項同餘方程的解
關於二項同餘方程(1)的解有如下結論：
1.設m>1，且有原根 ɡ，(a，m)=1，k≥1，則(1)有解的充分必要條件是(k，φ(m))|ind a，若有解，恰有(k，φ(m))個解。
2.設m>1，k≥1，(a，m)=1，模m有原根，則a是模m的k次剩餘的充分必要條件是
3.若m=2，α≥3，2∤a，
，則二項同餘方程x≡a(mod 2)當2∤ k時恰有一解；當2|k時有解的充分必要條件是r-1=0，且(k，2)|r0，若有解，恰有2(k，2)個解。
