二階線性雙曲型方程(second order linear hy- perbolic equation)最簡單最重要的雙曲型偏微分 方程.對於,+1個自變數t,x= (x
xz, """,二。)的二 階線性偏微分方程

假設所有係數及f都是t,x的光滑函式.如果在固 定點((t,x)處特徵方程
對任意非零實數組寧=+i,}z,...,}}>,恆有兩個相 異實根}, <t,二;}>,}Zct,x;}>,則稱1 u=0在點(t,二) 處為雙曲型方程,或簡稱在(<t,x>處是雙曲的.若在 所考查的區域的每點處1u=。都是雙曲的,則稱 Lu = 0在該區域是雙曲的.如果}i , }:關於((t,二) 任Q是一致分離的,即當
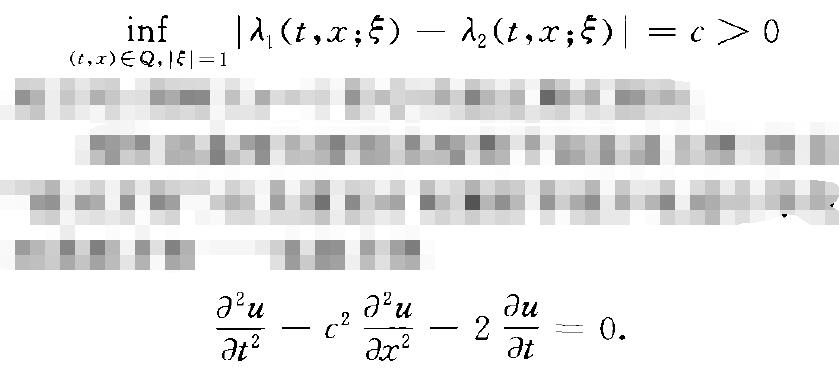
成立時,則稱Lu=0在Q內是正則雙曲的. 線性雙曲型方程的典型例子是波動方程(參見 “波動方程”)以及描述有電漏的導線中電流傳導的 雙曲型方程—電報方程
