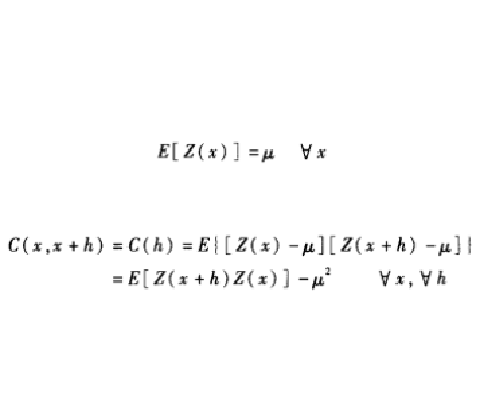二階平穩假設

二階平穩假設(second stationary assumption)亦稱弱平穩假設，是討論區域化變數Z(x)本身的特徵，這種平穩假設至少要求Z(x)的各階矩均存在且平穩，在實際工作中很難滿足。

基本介紹

• 中文名：二階平穩假設
• 外文名：second stationary assumption
• 別稱：弱平穩假設
• 所屬學科：數學（統計學）
• 相關概念：內蘊假設，區域化變數等

定義

當區域化變數滿足下列兩個條件時，則稱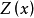滿足二階平穩(或弱半穩)：

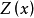
①在整個研究區域內，區域化變數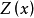的數學期望存在且不隨位置發生變化，即

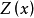
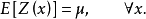
②在整個研究區域內，區域化變數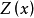的協方差函式存在，且僅依賴於滯後距離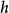，與無關，即

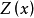
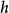
二階平穩假設假定研究區域化隨機變數的協方差存在，實際就是假設了區域化變數有一個有限的先驗方差。當時，有

對相關函式可寫成

二階平穩假設與本徵假設的比較

簡單而言，二階平穩假設是討論區域化變數本身的特徵，而本徵假設是研究區域化變數增量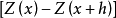的特徵。一般而言，二階平穩假設對區城化變數要求較嚴，本徵假設要求較弱。也就是說，如果某個研究區域區域化變數是二階平穩的，那么它一定是本徵的；反之，若是本徵的，則不一定是二階平穩。

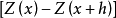
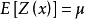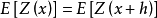由二階平穩假設的第一個條件，顯然可以推導出本徵假設的第一個條件，。但由本徵假設的第一個條件，只能推導出，無法肯定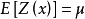是否成立。在一般情況下，對任意一組數據都可求出它們的均值，但這個均值並不一定等於這個研究區域的數學期望值。因此，本徵假設容許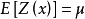不成立，所以區域化變數滿足本徵假設不一定滿足二階平穩假設。

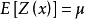
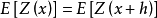
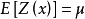
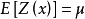
由二階平穩的兩個條件可以推導出本徵假設的第二個條件:

由上式可見，只要區域化變數的協方差存在，則半方差函式一定存在。為區域化變數的方差，即二階平穩假設事先暗示了區域化變數的方差存在，因此這個方差又稱為先驗方差。

準二階平穩假設及準本徵假設

如果區域化變數只在有限區城內是二階平穩的或是本徵的，則稱此區域化變數是準二階平穩的或準本徵的。準二階平穩或準本徵假設是一種折中方案，既要考慮到平穩或本徵的範圍大小，又要顧及有效數據的多少。如果範圍確定大了，往往不易滿足二階平穩或本徵假設的條件；若範圍確定太小，則區域內的數據就太少。放確定範圍的大小應兼顧上述兩方面。