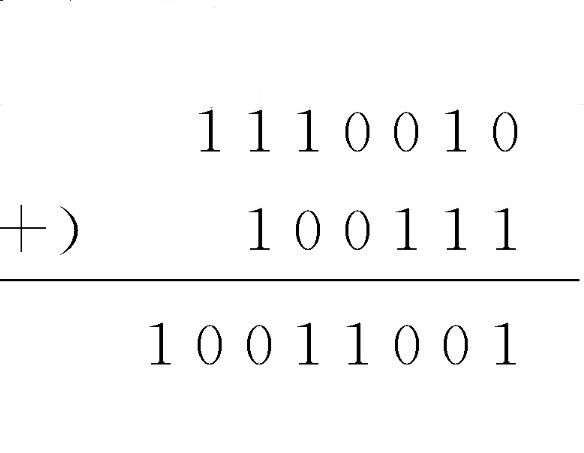二進數加法(addition of binary numbers)是二進數的計算方法之一,指計算二進數的和的方法,由於在二進制記數法中,任何相鄰兩數位之間的進率為2,所以加法按逢二進一,減法按退一當二的法則進行計算。
基本介紹
- 中文名:二進數加法
- 外文名:addition of binary numbers
- 所屬學科:數學
- 所屬問題:算術(命數法)
- 簡介:二進數的計算方法之一
基本介紹,二進數加法原則,算式舉例,相關說明,
基本介紹
二進制法是每進一位,位數以兩倍增加的數的表示方法。把二進制數以2的乘方展開的式子,稱為” 二進制的表達式”。若要把二進制數以十進制表示,則先將它以二進制的表達式展開後,再計算就可以得出。計算二進制的加法和減法時,若有位數變換,不管進位或借一都會得2。
二進數加法原則
一位二進數的加法形式有下列四種基本運算:
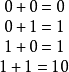

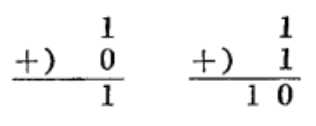
算式舉例
1.加法算式舉例,計算1110010(2)+100111(2)。

所以1110010(2)+100111(2)=10011001(2)。
2.減法算式舉例,計算10011001(2)-1110010(2)。

所以10011001(2)-1110010(2)=100111(2)。
相關說明
二進數主要用於電子計算機,但在電子計算機中進行減法運算時,為了避免因不夠減而產生退位的運算,就引入補數,化為加法來計算。若x(2)+y(2)=10(2),則y(2)稱為x(2)的補數,也就是要湊一個數y(2),使與x(2)相加後為10(2),n為二進數x(2)的位數。總之y(2)加到x(2)上能使x(2)的各位非零數1都通過進位消失而變為0。例如,x(2)=1010110右起第二個數位是第一次出現1,這時取y(2)的右兩位為10(即與x(2)的右兩位相同),於是x(2)+y(2)中的右起第二位相加時,要進1,故y(2)的其餘數位的數碼應取與x(2)同一數位上的與之不同的數碼,即y(2)的右起第三位為0(x(2)的右起第三位為1),第四、五、六、七位分別為1,0,1,0(x(2)的右起第四、五、六、七位各為0,1,0,1),得y(2)=0101010(2)=101010(2).根據上例的分析,求補數的方法歸納如下:
1.觀察x(2)的各位數字,從右第一位起到第一次出現1的數位為止,這時x(2)的補數y(2)在相同數位上應取與x(2)中同樣的數碼,如上例x(2)=1010110,從右第一位到第一次出現1為止的各位為10,則y(2)中的最末兩位數碼也應為10。
2.y(2)的其餘數位的數碼,應取與x(2)相同數位上不同的數碼,如上例x(2)=1010110中的其餘數位的數碼,即從右起第三位到最後一位的數碼為10101,則y(2)中與之對應的各數位應取和x(2)中對應數位上不同的數碼,即y(2)的其餘數位應取01010。又如x(2)=1001010(2),則y(2)=0110110(2)=110110(2)。有了補數,減法可化為加法進行,其公式為:被減數-減數=被減數+補數-10(2)。式中的補數是指減數的補數,n是減數的二進制位數。例如前面的減法中,計算10011001(2)-1110010(2)。可改為10011001(2)-1110010(2)=10011001(2)+1110(2)-10000000(2)=100111。如此就避免了退位計算,比直接相減更為簡單明了。