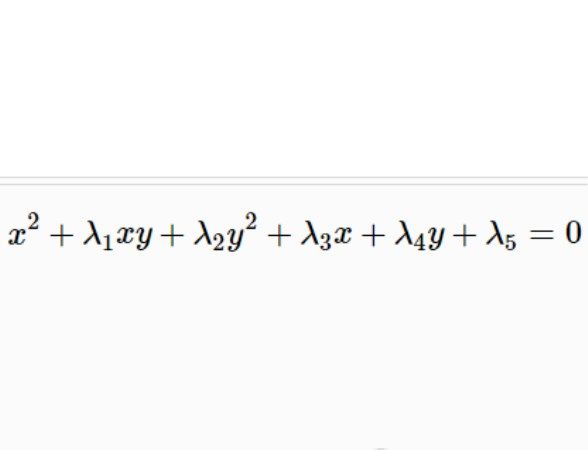二次曲線族

二次曲線族是二次曲線的集合，指具有某種共同性質的二次曲線的全體，它可簡化求適合一定條件的二次曲線的方程的步驟，隨著獨立參數個數的不同，把二次曲線族按其參數的個數而分為單參數二次曲線族、雙參數二次曲線族等。

基本介紹

• 中文名：二次曲線族
• 所屬學科：數學
• 所屬問題：平面幾何
• 簡介：具有某共同性質的二次曲線全體

基本概念

在二次曲線的方程

中，二次項的係數不全為零，不妨設a₁₁≠0,那么以a₁₁除方程兩邊，所得到的方程

仍然表示同一條曲線，這個方程中含有五個獨立的係數(亦稱參數)，如果給這些參數各種不同的數值，可得到各種不同的曲線，形成一族二次曲線，稱它為二次曲線族。又隨著獨立參數個數的不同，把二次曲線族按其參數的個數而分為單參數二次曲線族、雙參數二次曲線族等。例如:

如果二次方程(1)的參數滿足，那么這二次方程所含的獨立參數的個數就由五個減到三個而成為三參數二次曲線族，即圓族。

如果二次方程(1)的參數滿足 ,那么這二次方程所含的獨立參數的個數就由五個減到四個而成為四參數二次曲線族，即拋物線族。

如果二次方程(1)的參數滿足 ,那么這二次方程所含的獨立參數的個數並沒有減少，仍為五個獨立參數，是五參數二次曲線族，即中心二次曲線族。

二次曲線族可簡化求適合一定條件的二次曲線的方程的步驟：

1.給定兩條二次曲線F₁(x，y)=0，F₂(x，y)=0，經過這兩條二次曲線的所有交點(一般有4個)的二次曲線族的方程為λ₁F₁(x，y)+λ₂F₂(x，y)=0，式中λ₁，λ₂是不同時為零的參數。

2.經過兩條直線L_i=A_ix+B_iy+C_i=0(i=1，2)與二次曲線F(x，y)=0的交點的二次曲線族的方程為F(x，y)+λL₁L₂=0，式中λ是參數。

3.經過4點P_i(x_i，y_i)(i=1，2，3，4)的二次曲線族的方程為L₁₂L₃₄+λL₂₃L₄₁=0，式中λ是參數，L_i，i+1=(y_i+1-y_i)(x-x_i)-(x_i+1-x_i)(y-y_i)，x₅=x₁，y₅=y₁。

4.與已知兩直線L₁=0，L₂=0分別相切於已知點P₁(x₁，y₁)，P₂(x₂，y₂)的二次曲線族的方程為L₁₂+λL₁L₂=0，式中L₁₂=(y₂-y₁)(x-x₁)-(x₂-x₁)(y-y₁)，λ是參數，例如，已知A(-1，0)，B(1，0)，C(a，b)和AB邊上的中線OC上一點P，OP/OC=f，則與兩直線AC，BC分別相切於點A，B，且過點P的二次曲線為fbx-2fabxy+(fa+1-2f)y+2fby-fb=0，當f=1/2時，圖形為拋物線；當0<f<1/2時，圖形為橢圓；當1/2<f<1時，圖形為雙曲線。

5.與二次曲線F(x，y)=0相切於已知點(a，b)(F(a，b)=0)的二次曲線族的方程為F(x，y)+λ(x-a)+μ(y-b)=0，式中λ，μ是參數，λ+μ≠0。

二次曲線族的相關定理

下面僅討論單參數二次曲線族，又稱為二次曲線系。

定理1 如果給定兩條二次曲線，那么含有一個參數λ的方程：

f₁(x,y)+λf₂(x,y)=0， (1)

是表示經過這兩條二次曲線的所有交點(一般有四個)的二次曲線族，為了避免將曲線 遺漏掉，也將這二次曲線族的方程寫成

λ₁f₁(x,y)+λ₂f₂(x,y)=0， (1')

定理1的證明過程與直線系的定理證明相仿。

定理2 如果已知兩直線L_i≡a_ix +b_iy+c_i=0(i=1,2)和一條二次曲線f(x,y)=0，那么含有一個參數λ的方程

f(x,y)+λL₁L₂=0， (2)

是表示經過兩直線與二次曲線的交點的二次曲線族。

證明 因為直線L_i=0(i=1，2)與二次曲線f(x,y)=0的交點坐標滿足式(2),所以曲線(2)過它們的交點，又方程(2)的次數不大於二次，所以，它是單參數二次曲線族。

定理3如果已知四點經過點的直線方程為(這裡i=1,2,3,4,i+1=2,3,4,1)，那么含有一個參數的方程

是表示經過這四點的二次曲線族。

定理4 與已知直線L₁=0，L₂=0分別相切於已知點P₁，P₂的二次曲線族的方程為

這裡直線的方程是L₁₂=0。