二次曲線三角形調和定理

二次曲線的三角形調和定理：

外切於二次曲線的三角形的一條邊的兩端點被這條邊的切點和這條邊和另兩條邊的切點的連線的交點調和分離。

二次曲線的三角形調和定理的對偶定理為：

內接於二次曲線的三角形的一個頂點上的兩條邊被這個頂點處的切線和這個頂點和另兩點處的切線的交點的連線調和分離。

基本介紹

• 中文名：二次曲線的三角形調和定理
• 提出者：程浩
• 提出時間：2020年7月23日
• 適用領域：幾何

推導過程

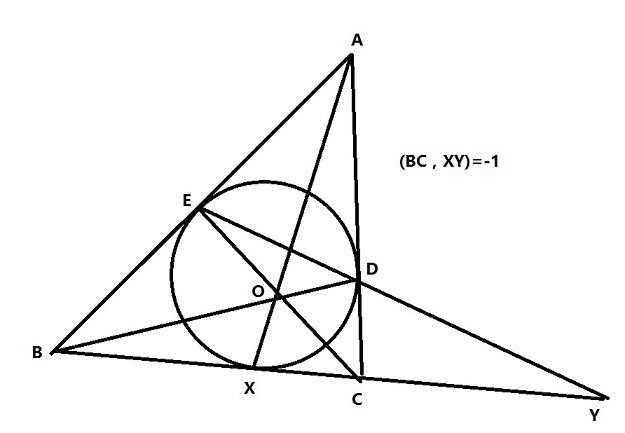
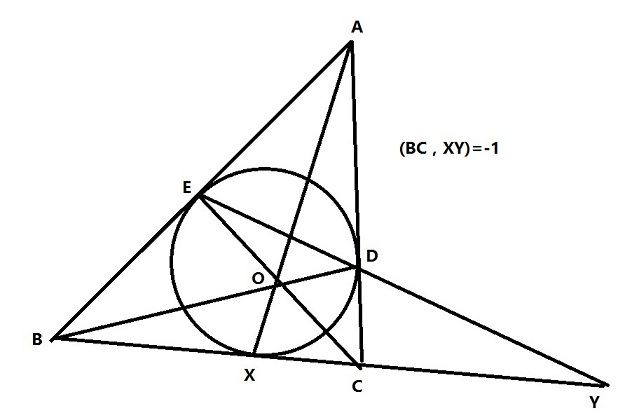
BC被XY調和分離

三角形ABC外切於二次曲線，切點為D，E，X

則AX和BD和CE交於一點O（布利安桑定理）

考察完全四點形AEOD

AE和OD的交點為B

AD和EO的交點為C

AO和BC的交點為X

ED和BC的交點為Y

則BC被XY調和分離

(BC,XY)=-1

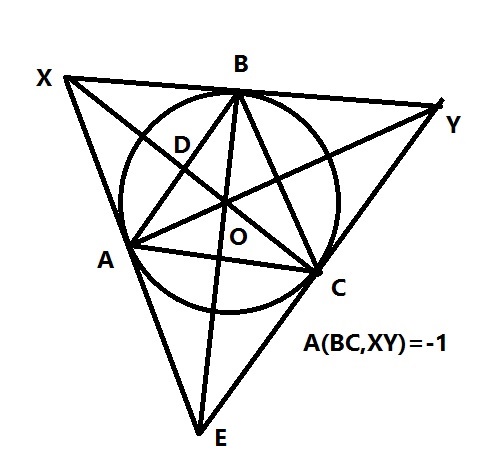
AB和AC被AX和AY調和分離

三角形ABC內接於二次曲線，

過A點和B點和C點做曲線的切線，

A點處的切線和B點處的切線交於點X

B點處的切線和C點處的切線交於點Y

A點處的切線和C點處的切線交於點E

則AY和BE和CX交於一點O（布利安桑定理）

考察完全四點形BOCY

BY和CO的交點為X

BO和CY的交點為E

YO和XE的交點為A

則CD被XO調和分離

既AB和AC被AX和AY調和分離

A(BC,XY)=-1

套用

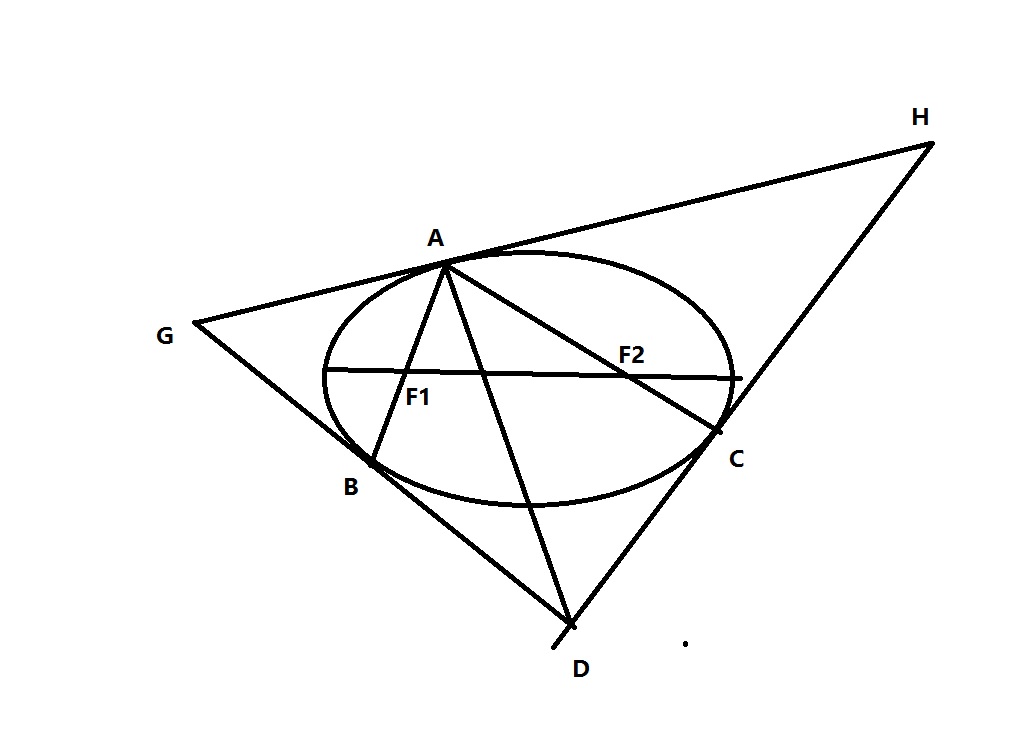
二次曲線三角形調和定理的套用例子

證明圓錐曲線的內接焦點三角形定理：

根據二次曲線三角形調和定理

A（BC,GD）=-1

設A點處的切線為GH，法線為AD’

又因為圓錐曲線的光學性質

角BAD'=角CAD'

AD垂直於GH

也就是AD'是角BAC的內角平分線

GH是角BAC的外角平分線

所以A（BC,GD'）=-1

所以AD和AD‘重合

既是A點處的法線和B處切線和C處切線三線共點。