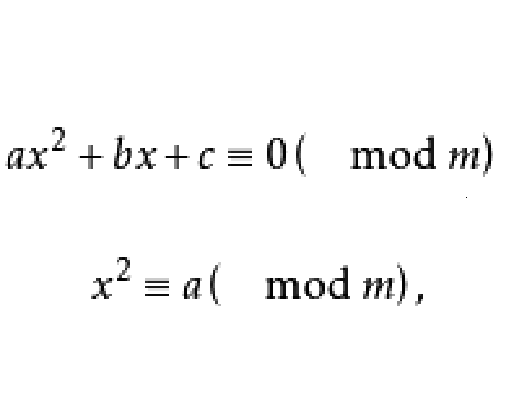二次同餘式

二次同餘式(quadratic congruence)亦稱二次同餘方程，是一類同餘方程，它是關於未知數的二次多項式的同餘方程。二次同餘式是研究高次同餘式的基礎，在密碼學中套用很廣泛。一般的二次同餘式求解問題可以歸結到討論形如x≡a(mod m)的同餘式。

基本介紹

• 中文名：二次同餘式
• 外文名：quadratic congruence
• 別稱：二次同餘方程
• 屬性：一類同餘方程
• 相關概念：二次剩餘，二次非剩餘等

基本介紹

二次同餘式是關於未知數的二次多項式的同餘方程。設正整數 ，且 ，則稱形如

的同餘式為二次同餘式的一般形式，簡稱模m的二次同餘式。此外，稱形如

的同餘式為最簡二次同餘式，或稱最簡二次同餘方程。滿足同餘式(1)或(2)的 值，分別稱為二次同餘式(1)或(2)的解，亦稱二次同餘式的根。若 為其一解，則 均為其解，即是說若 適契約餘式(1)或(2)，則 所代表的剩餘類中的每一個數皆能適合(1)式或(2)式，但常指該類中的最小正整數為其解，故方程(1)或(2)的解的個數，系指不同剩餘類中的能適合(1)式或(2)式的解之個數。二次同餘式不一定都有解，如果有解時，其解的個數參見下文“二次同餘式的解數”。

注意：用 乘式(1)再加上 ，得

即

若令 ，則上式變為

由同餘式的性質可知式(1)與式(3)同時有解或同時無解：故討論式(1)有解的問題可以轉為討論式(3)有解的問題。

二次同餘式的解數

二次同餘式的解數(solution numbers of a quadratic congruence)是對二次同餘式的一種刻畫，即二次同餘方程解的個數的判定：設 為素數， ，且 ，二次同餘式

在 時，解的個數為 。

在 時，解的個數有下面三種情形：

1. ，有一個解；

2. ，當 時有二解， 時無解；

3. ，當 時有四解， 時無解。

二次剩餘與二次非剩餘

為了討論式(3)是否有解，引入了二次剩餘和二次非剩餘的概念。

定義設m是正整數，若同餘式

有解，則 稱為模m的二次剩餘(或二次剩餘)；否則， 稱為模m的二次非剩餘(或二次非剩餘)。

下面我們先來討論模為奇素數p的二次同餘式

定理1(歐拉判別條件)設p是奇素數， ，則

(1) 是模p的二次剩餘的充分必要條件是

(2) 是模p的二次非剩餘的充分必要條件是

並且當 是模p的二次剩餘時，式(5)恰有二解。

推論 設p是奇素數， ，則

(1) 如果 都是模p的二次剩餘，則 是模p的二次剩餘；

(2) 如果 都是模p的二次非剩餘，則 是模p的二次剩餘；

(3) 如果 是模p的二次剩餘，而 是模p的二次非剩餘，則 是模p的二次非剩餘。

定理2 設p是奇素數，則模p的簡化剩餘系中二次剩餘與二次非剩餘的個數各為，且個二次剩餘與序列

中的一個數同餘，且僅與一個數同餘。