二叉圖

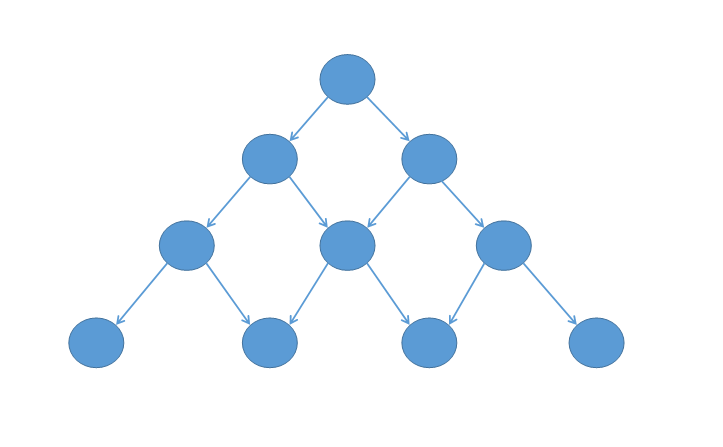
二叉圖（Binary-Graph），一種C++14規範中引入的高級數據結構。其集合了二叉樹和圖論的優點，在世界算法數據結構大會上由斯茂·斯迪尤德恩特首先提出。 二叉圖在形式上類似於二叉樹，其實現類似於圖論。

其形式近似於完全連通的楊輝三角或子節點重合的完全二叉樹，在時間操作上遍歷可以達到O（nlog1/n）的極低複雜度。適用於LCA查詢任意點，在實現大規模數據時建樹複雜度近似級數求和。雖然稱作二叉，但其實際上是圖論適用的內容，廣泛適用於各大領域，在最佳化近似堆維護SPFA等算法上都有套用。完全二叉圖和滿二叉圖的原理類似，但極易由於數據退化，

基本介紹

• 中文名：二叉圖
• 外文名：Binary-Graph
• 性質：高級數據結構
• 所屬程式：C++

一、定義

二叉圖（Binary-Map），一種C++14規範中引入的高級數據結構。其集合了二叉樹和圖論的優點，在世界算法數據結構大會上由斯茂·斯迪尤德恩特首先提出。
二叉圖在形式上類似於二叉樹，其實現類似於圖論（在下面的代碼中有介紹）。由N個點，E條邊構成，E在等於N-1時二叉圖的複雜度退化為二叉樹，其主要特徵是二叉圖的深度為depth以下的點中可以以圖的方式兩兩連線，並忽略其中邊權，直接理解為兩點重合，從而達到以二叉形式實現連通環的目的。
其形式近似於完全連通的楊輝三角或子節點重合的完全二叉樹，在時間操作上遍歷可以達到O（nlog1/n）的極低複雜度。適用於LCA查詢任意點，在實現大規模數據時建樹複雜度近似級數求和。
雖然稱作二叉，但其實際上是圖論適用的內容，廣泛適用於各大領域，在最佳化近似堆維護SPFA等算法上都有套用。
完全二叉圖和滿二叉圖的原理類似，但極易由於數據退化，因此這裡不作探討。

二、STL實現

binary_map<pair<int,int> > q;q.push_back(make_pair(u,v))//建邊q.push_front(make_pair(u,v))//建邊這兩個都是建邊，但是可能導致遍歷的方式不同q.find_root()//return 圖的根節點q.size()//return 圖的大小q.get_depth()//return 圖的深度q.empty()//如果圖為空，return false，否則，return true;q.top()//return 是pair<int,int>型的邊q.back()//return 是pair<int,int>型的邊區別同push_back與push_frontq.pop()//根據前序遍歷彈出第一個點q.back_pop()//根據後序遍歷彈出第一個點q.begin()//return iterator型的指針，返回第一個數據q.end()//return iterator型的指針，返回最後一個數據q.__lca(int x,int y)//return a與b的最近公共點priority_binarymap<pair<int,int> >q;由於優先二叉圖具有的性質類似於優先佇列，內部用斐波那契堆維護，不過只能從一頭取出元素。q.push(make_pair<u,v>);//將一條邊放入堆內q.top();//返回邊權值最小的一條邊，返回的類型是pair<int,int>q.pop();//彈出堆頂的元素q.empty();//如果圖為空，則返回false，否則，返回true同時與優先佇列相同，也有小根堆priority_binarymap<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> >

三、二叉圖的套用

這裡需要先引進一個概念，二叉圖的重心。
該重心的概念是和該數據結構同時在大會上提出的，重心的概念類似於信息學中的數據結構的樹的重心。
其主要意義出自於其幾何概念，實現由C++的標準庫進行。
二叉圖的重心通過深度優先搜尋來遍歷，從而實現了該二叉圖邊權的中心搜尋，在最大流和二叉圖對稱完備匹配中有廣泛的套用。

struct node{        int lc,rc;     int value;}binary_map[N];int dis[N][N];int dfs(int root){            int lc,int rc;        if(binary_map[root].lc)            lc+=dfs(binary_map[root].lc)+dis[root][binary_map[root].lc];         else                        return 0;        if(binary_map[root].rc)                        rc+=dfs(binary_map[root].rc)+dis[root][binary_map[root].rc];        else                        return 0;                binary_map[root].value=lc+rc; }遍歷binary_map中,排序後求lc與rc比例，中間數即為該圖的重心值，所屬節點即為重心。