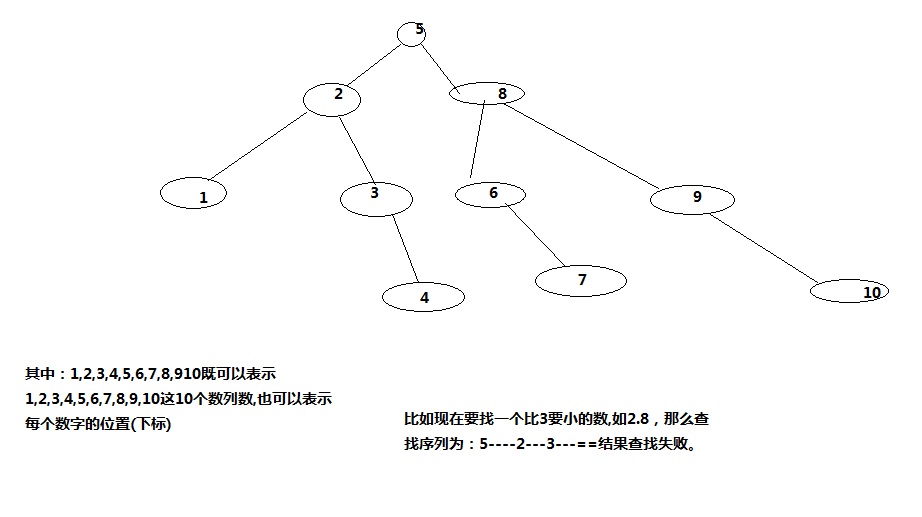
算法:二分法查找適用於數據量較大時,但是數據需要先排好順序。主要思想是:(設查找的數組區間為array[low, high])
(1)確定該區間的中間位置K(2)將查找的值T與array[k]比較。若相等,查找成功返回此位置;否則確定新的查找區域,繼續二分查找。區域確定如下:a.array[k]>T 由數組的有序性可知array[k,k+1,……,high]>T;故新的區間為array[low,……,K-1]b.array[k]<T 類似上面查找區間為array[k+1,……,high]。每一次查找與中間值比較,可以確定是否查找成功,不成功當前查找區間將縮小一半,遞歸查找即可。時間複雜度為:O(log2n)。
基本介紹
- 中文名:二分法查找
- 外文名:Binary Search
- 類別:查找算法
- 要求:數組中元素是有順序的
- 主要思想:對序列進行遞歸(或循環查找)
算法,算法複雜度分析,時間複雜度,空間複雜度,java代碼,C代碼,C++代碼,php代碼,Python代碼,
算法
[一維數組,折半查找]
假如有一組數為3,12,24,36,55,68,75,88要查給定的值24.可設三個變數front,mid,end分別指向數據的上界,中間和下界,mid=(front+end)/2.
1.開始令front=0(指向3),end=7(指向88),則mid=3(指向36)。因為a[mid]>x,故應在前半段中查找。
2.令新的end=mid-1=2,而front=0不變,則新的mid=1。此時x>a[mid],故確定應在後半段中查找。
3.令新的front=mid+1=2,而end=2不變,則新的mid=2,此時a[mid]=x,查找成功。
如果要查找的數不是數列中的數,例如x=25,當第三次判斷時,x>a[mid],按以上規律,令front=mid+1,即front=3,出現front>end的情況,表示查找不成功。
例:在有序的有N個元素的數組中查找用戶輸進去的數據x。
算法如下:
1.確定查找範圍front=0,end=N-1,計算中項mid=(front+end)/2。
2.若a[mid]=x或front>=end,則結束查找;否則,向下繼續。
3.若a[mid]<x,說明待查找的元素值只可能在比中項元素大的範圍內,則把mid+1的值賦給front,並重新計算mid,轉去執行步驟2;若a[mid]>x,說明待查找的元素值只可能在比中項元素小的範圍內,則把mid-1的值賦給end,並重新計算mid,轉去執行步驟2。
算法複雜度分析
時間複雜度
1.最壞情況查找最後一個元素(或者第一個元素)Master定理T(n)=T(n/2)+O(1)所以T(n)=O(log2n)
2.最好情況查找中間元素O(1)查找的元素即為中間元素(奇數長度數列的正中間,偶數長度數列的中間靠左的元素)
空間複雜度
- S(n)=logn
java代碼
public class BinaryTest{ public static int binary(int[] array, int value) { int low = 0; int high = array.length - 1; while(low <= high) { int middle = (low + high) / 2; if(value == array[middle]) { return middle; } if(value > array[middle]) { low = middle + 1; } if(value < array[middle]) { high = middle - 1; } } return -1; } public static void main(String[] args) { int[] a = {1, 2, 3, 4, 5, 6, 7, 8, 9}; int value = binary(a, 9); System.out.println(value); }}C代碼
#include<stdio.h>//遞歸算法int recurbinary(int *a, int key, int low, int high){ int mid; if(low > high) return -1; mid = low + (high-low)/2; if(a[mid] == key) return mid; else if(a[mid] > key) return recurbinary(a,key,low,mid -1); else return recurbinary(a,key,mid + 1,high);}//非遞歸算法int binary( int *a, int key, int n ){ int left = 0, right = n - 1, mid = 0; mid = left + (right - left) / 2; while( left < right && a[mid] != key ) { if( a[mid] < key ) { left = mid + 1; } else if( a[mid] > key ) { right = mid; } mid = ( left + right ) / 2; } if( a[mid] == key ) return mid; return -1;}int main(){ int a[] = {1,2,3,4,5,6,7,8,9,12,13,45,67,89,99,101,111,123,134,565,677}; int b[] = {677,1,7,11,67}; int i; for( i=0; i<sizeof(b)/sizeof(b[0]); i++ ) { //printf( "%d\n", recurbinary(a, b[i],0,sizeof(a)/sizeof(a[0])-1) ); printf( "%d\n", binary( a, b[i], sizeof(a)/sizeof(a[0]))); } return 0;}C++代碼
#include<iostream>#define N 10using namespace std;int main(){ int a[N],front,end,mid,x,i; cout<<"請輸入已排好序的a數組元素:"<<endl; for(i=0;i<N;i++) cin>>a[i]; cout<<"請輸入待查找的數x:"<<endl; cin>>x; front=0; end=N-1; mid=(front+end)/2; while(front<end&&a[mid]!=x) { if(a[mid]<x)front=mid+1; if(a[mid]>x)end=mid-1; mid=(front+end)/2; } if(a[mid]!=x) cout<<"沒找到!"<<endl; else cout<<"找到了,在第"<<mid+1<<"項里"<<endl; return 0;}php代碼
<?phpfunction binarySearch($array, $val) { $count = count($array); $low = 0; $high = $count - 1; while ($low <= $high) { $mid = intval(($low + $high) / 2); if ($array[$mid] == $val) { return $mid; } if ($array[$mid] < $val) { $low = $mid + 1; } else { $high = $mid - 1; } } return false;}Python代碼
mylist = [20,50,22,-22,0,15,222,28,29,99,1999,100823,55,35,5,1,2,3,8,9,55,10239,234234]def lgfind(arr,v): arr = sorted(arr)#排序數組,從小到大 print(arr) start = 0 #變數開始 arrLen = len(arr)-1 #變數結束 while( start <= arrLen ): mid = (start + arrLen) // 2 #變數中間值 print('mid',mid) #如果中間的找到直接返回 if arr[mid] == v: return v #比對大小,看看我們要的結果是在上半段,還是下半段 if arr[mid] > v: arrLen= mid - 1 #結果在上半段 else: start= mid + 1 #結果在下半段 return false #沒有則返回假 have = lgfind(mylist,28)print(have)