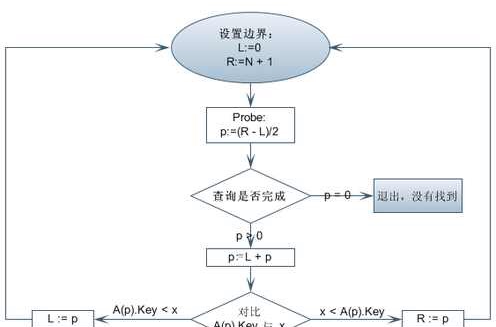
二分查找也稱折半查找(Binary Search),它是一種效率較高的查找方法。但是,折半查找要求線性表必須採用順序存儲結構,而且表中元素按關鍵字有序排列。
基本介紹
- 中文名:二分查找
- 外文名:Binary Search
- 別稱:折半查找
- 提出者:John Mauchly
- 提出時間:1946
- 套用學科:計算機
- 適用領域範圍:程式語言
- 優點:查找速度快
- 缺點:待查表為有序表
- 時間複雜度:O(log2n)
查找過程,算法要求,比較次數,算法複雜度,代碼示例,
查找過程
首先,假設表中元素是按升序排列,將表中間位置記錄的關鍵字與查找關鍵字比較,如果兩者相等,則查找成功;否則利用中間位置記錄將表分成前、後兩個子表,如果中間位置記錄的關鍵字大於查找關鍵字,則進一步查找前一子表,否則進一步查找後一子表。重複以上過程,直到找到滿足條件的記錄,使查找成功,或直到子表不存在為止,此時查找不成功。
算法要求
1.必須採用順序存儲結構。
2.必須按關鍵字大小有序排列。
比較次數
計算公式: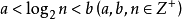
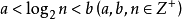
當順序表有n個關鍵字時:
查找失敗時,至少比較a次關鍵字;查找成功時,最多比較關鍵字次數是b。
注意:a,b,n均為正整數。
算法複雜度
二分查找的基本思想是將n個元素分成大致相等的兩部分,取a[n/2]與x做比較,如果x=a[n/2],則找到x,算法中止;如果x<a[n/2],則只要在數組a的左半部分繼續搜尋x,如果x>a[n/2],則只要在數組a的右半部搜尋x.
時間複雜度無非就是while循環的次數!
總共有n個元素,
漸漸跟下去就是n,n/2,n/4,....n/2^k(接下來操作元素的剩餘個數),其中k就是循環的次數
由於你n/2^k取整後>=1
即令n/2^k=1
可得k=log2n,(是以2為底,n的對數)
所以時間複雜度可以表示O(h)=O(log2n)
下面提供一段二分查找實現的偽代碼:
BinarySearch(max,min,des)
mid-<(max+min)/2
while(min<=max)
mid=(min+max)/2
if mid=des then
return mid
elseif mid >des then
max=mid-1
else
min=mid+1
return max
折半查找法也稱為二分查找法,它充分利用了元素間的次序關係,採用分治策略,可在最壞的情況下用O(log n)完成搜尋任務。它的基本思想是:(這裡假設數組元素呈升序排列)將n個元素分成個數大致相同的兩半,取a[n/2]與欲查找的x作比較,如果x=a[n/2]則找到x,算法終止;如 果x<a[n/2],則我們只要在數組a的左半部繼續搜尋x;如果x>a[n/2],則我們只要在數組a的右 半部繼續搜尋x。
代碼示例
C#代碼
public static int Method(int[] nums, int low, int high, int target) { while (low <= high) { int middle = (low + high) / 2; if (target == nums[middle]) { return middle; } else if (target > nums[middle]) { low = middle + 1; } else if (target < nums[middle]) { high = middle - 1; } } return -1; }Go原始碼
func binarySearch(checkSlice []int, findVal int) int { pos := -1 left, right := 0, len(checkSlice) //此處right長度不減1 , 如果最大值為查找值,此處減一代碼進入死循環Loop: for { if(left >= right){ break Loop } mid := (left + right) / 2 switch true { case checkSlice[mid] < findVal : left = mid case checkSlice[mid] == findVal : pos = mid break Loop case checkSlice[mid] > findVal : right = mid } } return pos}Swift原始碼
func binarySearch<T: Comparable>(_ a: [T], key: T) -> Int? { var lowerBound = 0 var upperBound = a.count while lowerBound < upperBound { let midIndex = lowerBound + (upperBound - lowerBound) / 2 if a[midIndex] == key { return midIndex } else if a[midIndex] < key { lowerBound = midIndex + 1 } else { upperBound = midIndex } } return nil}Python原始碼
def bin_search(data_list, val): low = 0 # 最小數下標 high = len(data_list) - 1 # 最大數下標 while low <= high: mid = (low + high) // 2 # 中間數下標 if data_list[mid] == val: # 如果中間數下標等於val, 返回 return mid elif data_list[mid] > val: # 如果val在中間數左邊, 移動high下標 high = mid - 1 else: # 如果val在中間數右邊, 移動low下標 low = mid + 1 return # val不存在, 返回Noneret = bin_search(list(range(1, 10)), 3)print(ret)
pascal原始碼
第一種
programjjzx(input,output);vara:array[1..10]ofinteger;i,j,n,x:integer;begin['輸入10個從小到大的數:']for i:=1 to 10 do read(a[i]);['輸入要查找的數:']readln(x);i:=1;n:=10;j:=trunc((i+n)/2);repeatif a[j]>x thenbeginn:=j-1;j:=trunc((i+n)/2)endelse if a[j]<x thenbegini:=j+1;j:=trunc((i+n)/2)end;until(a[j]=x)or(i>=n);{為什麼是這個結束循環條件——i>n表示所查找的範圍已經空了(就是沒找到)}if a[j]=x thenwriteln('查找成功!位置是:',j:3)elsewriteln('查找失敗,數組中無此元素!')end.第二種
var a:array[1..100001] of longint; n,m,i,t:longint; function search(k:longint):longint;var l,r,mid:longint;begin l:=1; r:=n; mid:=(l+r) div 2; while (a[mid]<>k) and (l<=r) do begin if a[mid]>k then r:=mid-1 else l:=mid+1; mid:=(l+r) div 2; end; if l>r then exit(0); exit(mid);end;begin readln(n,m); for i:=1 to n do read(a[i]); for i:=1 to n do begin read(t); if search(t)=0 then writeln('no') else writeln(search(t)); end;end.C和C++代碼
<C和C++的語法基本相同>
循環實現
第一種
int BinSearch(SeqList *R,int n,KeyType K){ //在有序表R[0..n-1]中進行二分查找,成功時返回結點的位置,失敗時返回-1 int low=0,high=n-1,mid; //置當前查找區間上、下界的初值 while(low<=high) { if(R[low].key==K) return low; if(R[high].key==k) return high; //當前查找區間R[low..high]非空 mid=low+(high-low)/2; /*使用(low+high)/2會有整數溢出的問題 (問題會出現在當low+high的結果大於表達式結果類型所能表示的最大值時, 這樣,產生溢出後再/2是不會產生正確結果的,而low+((high-low)/2) 不存在這個問題*/ if(R[mid].key==K) return mid; //查找成功返回 if(R[mid].key<K) low=mid+1; //繼續在R[mid+1..high]中查找 else high=mid-1; //繼續在R[low..mid-1]中查找 } if(low>high) return -1;//當low>high時表示所查找區間內沒有結果,查找失敗}第二種
int bsearchWithoutRecursion(int array[],int low,int high,int target){ while(low<=high) { int mid=low+(high-low)/2;//還是溢出問題 if(array[mid]>target) high=mid-1; else if(array[mid]<target) low=mid+1; else return mid; } return-1;}第三種
int binSearch(const int *Array,int start,int end,int key){ int left,right; int mid; left=start; right=end; while(left<=right) { mid=left+(right-left)/2;//還是溢出問題 if(key==Array[mid]) return mid; else if(key<Array[mid]) right=mid-1; else if(key>Array[mid]) left=mid+1; } return -1;}遞歸實現(可直接編譯)
#include<iostream>using namespace std;int a[100]={1,2,3,5,12,12,12,15,29,55};//數組中的數(由小到大)int k;//要找的數字int found(int x,int y){ int m=x+(y-x)/2; if(x>y)//查找完畢沒有找到答案,返回-1 return -1; else { if(a[m]==k) return m;//找到!返回位置. else if(a[m]>k) return found(x,m-1);//找左邊 else return found(m+1,y);//找右邊 }}int main() { cin>>k;//輸入要找的數字c語言把cin換為scanf即可 cout<<found(0,9);//從數組a[0]到a[9]c語言把cout換為printf即可 return 0; }Java代碼
public static int binarySearch(Integer[] srcArray, int des) { //定義初始最小、最大索引 int start = 0; int end = srcArray.length - 1; //確保不會出現重複查找,越界 while (start <= end) { //計算出中間索引值 int middle = (end + start)>>>1 ;//防止溢出 if (des == srcArray[middle]) { return middle; //判斷下限 } else if (des < srcArray[middle]) { end = middle - 1; //判斷上限 } else { start = middle + 1; } } //若沒有,則返回-1 return -1;}AAuto代碼
//二分查找functionbinSearch(t,v){varp=#t;varp2;varb=0;do{p2=p;p=b+math.floor((p-b)/2)//二分折半運算if(p==b)return;if(t[p]<v){//判斷下限b=p;p=p2;}}while(t[p]>v)//判斷上限returnt[p]==v&&p;}//測試tab={}//創建數組,每個元素都是隨機數for(i=1;10;1){tab[i]=math.random(1,10000)}//插入一個已知數table.push(tab,5632)//排序table.sort(tab)io.open()io.print("數組",table.tostring(tab))io.print("使用二分查找,找到5632在位置:",binSearch(tab,5632))}PHP代碼
function binsearch($x,$a){ $c=count($a); $lower=0; $high=$c-1; while($lower<=$high){ $middle=intval(($lower+$high)/2); if($a[$middle]>$x){ $high=$middle-1; } elseif($a[$middle]<$x){ $lower=$middle+1; } else{ return $middle; } } return -1;}AS3代碼
publicstaticfunctionbinSearch(list:Array,low:int,high:int,key:int):int{if(low>high)return-1;varmid:int=low+int((high-low)/2);varindex:int=-1if(list[mid]==key){index=mid;}elseif(list[mid]<key){low=mid+1;index=binSearch(list,low,high,key);}else{high=mid-1;index=binSearch(list,low,high,key);}returnindex;}JavaScript代碼
var Arr = [3, 5, 6, 7, 9, 12, 15];function binary(find, arr, low, high) { if (low <= high) { if (arr[low] == find) { return low; } if (arr[high] == find) { return high; } var mid = Math.ceil((high + low) / 2); if (arr[mid] == find) { return mid; } else if (arr[mid] > find) { return binary(find, arr, low, mid - 1); } else { return binary(find, arr, mid + 1, high); } } return -1;}binary(15, Arr, 0, Arr.length - 1);PHP代碼
/*二分查找:前提,該數組已經是一個有序數組,必須先排序,再查找。*/function binarySearch(&$array,$findVal,$leftIndex,$rightIndex){$middleIndex=round(($rightIndex+$leftIndex)/2);if($leftIndex>$rightIndex){echo'查無此數<br/>';return;}if($findVal>$array[$middleIndex]){binarySearch($array,$findVal,$middleIndex+1,$rightIndex);}elseif($findVal<$array[$middleIndex]){binarySearch($array,$findVal,$leftIndex,$middleIndex-1);}else{echo"找到數據:index=$middleIndex;value=$array[$middleIndex]<br/>";if($array[$middleIndex+1]==$array[$middleIndex]&&$leftIndex<$rightIndex){binarySearch($array,$findVal,$middleIndex+1,$rightIndex);}if($array[$middleIndex-1]==$array[$middleIndex]&&$leftIndex<$rightIndex){binarySearch($array,$findVal,$leftIndex,$middleIndex-1);}}}