基本介紹
算法思想,算法描述,
算法思想
丹·科恩和伊凡·蘇澤蘭直線段裁剪主要分三步進行。
1．將矩形視窗四條邊界延長，則整個被平面分成九個區域，如圖1所示；
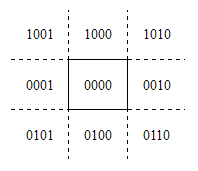圖1 區域劃分及編碼每個區域內的點都對應著一個四位二進制區位碼，其各位含義如如圖2所示。
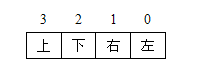圖2 區位碼各位含義任何位賦值1，代表端點落在相應的位置上，否則該位置為0。例如，如果端點在裁剪視窗內，則區位碼為0000，如果端點在矩形裁剪視窗的左下角，則區位碼為0101。
根據要裁剪線段P1P2的端點坐標求出相應的編碼值C1和C2。
2．判斷P1、P2的位置。
若C1=C2=0，即P1、P2的編碼全為零，線段P1P2在視窗內，保留線段P1P2，過程結束。
否則，若C1∧C2≠0，即作P1、P2編碼的邏輯與，結果為非零時，表示P1、P2在視窗的同側，棄之，過程結束。
否則，線段必有一端點在視窗外，令該點為P1，進行下一步。
3．根據P1點的編碼值，確定其在哪條邊界線之外，求線段與該邊界線的交點P，交點把線段分成兩段，捨去P1P段，把交點P作為剩餘線段的P1端點重新進行第二步。
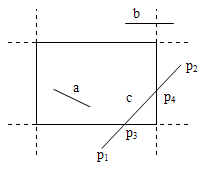圖3 丹·科恩和伊凡·蘇澤蘭算法示意圖如圖3所示，線段a經第二步測試為視窗內線段（C1=C2=0），取之。線段b經第二步測試為視窗外同側線段（C1∧C2≠0），棄之。線段c需在第三步求出與視窗邊界的交點P3，捨去P1P3段，把P3作為新的P1再進行第二步測試，又到第三步求出與視窗邊界的交點P4，捨去P4P2段，再把P4作為新的P2，經第二步測試為視窗內線段，取之。
算法描述
丹·科恩和伊凡·蘇澤蘭直線段裁剪算法的C語言描述如下。
#define LEFT 1#define TOP 8#define RIGHT 2#define BOTTOM 4void encode(x,y,color)float x,y;int *code;{ int c=0; if(x<XL)c=c| LEFT; else if(x>XR)c=c|RIGHT; if(y<YB)c=c|BOTTOM; else if(y>YT)c=c|TOP; *code=c; return;}void Swappoint(x1,y1,x2,y2)float *x1,*y1,*x2*,x2;{ float t; t=*x1;*x1=*x2;*x2=t; t=*y1;*y1=*y2;*y2=t;}void SwapCode(code1,code2)int *code1,*code2;{ int t; t=*code1;*code1=*code2;*code2=t;}/*(x1,y1)與(x2,y2)是線段端點坐標，其他四個參數分別為視窗左、右、上、下四個邊界*/C_S_Line_Clip(x1,y1,x2,y2, XL, XR,YT, YB)float x1,y1,x2,y2, XL, XR,YT, YB;{ int code1,code2,code; encode(x1,y1,&code1); encode(x2,y2,&code2); while(code1!=0&&code2!=0) { if(code1&code2!=0) return; if(code1==0) { SwapPoint(&x1,&y1,&x2,&y2); SwapCode(&code1,&code2); } code=code1; if(LEFT&code!=0)/*線段與左邊界相交*/ { x=XL; y=y1+(y2-y1)*(XL-x1)/(x2-x1); } else if(RIGHT&code!=0) /*線段與右邊界相交*/ { x=XR; y=y1+(y2-y1)*(XR-x1)/(x2-x1); } else if(TOP&code!=0) /*線段與上邊界相交*/ { y=YT; x=x1+(x2-x1)*(YT-y1)/(y2-y1); } else if(BOTTOM&code!=0) /*線段與下邊界相交*/ { y=YB; x=x1+(x2-x1)*(YB-y1)/(y2-y1); } x1=x; y1=y; encode(x,y,code1); } line(x1,y1,x2,y2);}