在計算機圖形學中,中點圓算法是一種用於確定繪製一個圓所需的像素點的算法。
基本介紹
- 中文名:中點圓算法
- 外文名:Midpoint circle algorithm
- 別稱:Bresenham's circle algorithm
- 提出者:Pitteway and Van Aken
- 套用學科:Computer science
- 適用領域範圍:繪圖
算法概念,準備工作,算法演示,實現過程,算法偽代碼,
算法概念
該算法的目標是找到一個通過使用像素格線的使得每個像素點儘可能接近x ^ 2 + y ^ 2 = r ^ 2的路徑。
準備工作
由於圓具有對稱性,所以我們只要考慮1/8個圓即可,我們選擇y軸正方向到延其順時針旋轉45°的這個區間為例。
我們先假設要畫的圓的圓心在坐標原點,最後再平移到其應該存在的位置。
設要畫的圓的圓心在原點(0,0),半徑為R,起點在(0,R)處,終點在( ,
, )處,順時針生成八分之一圓,利用對稱性畫出全部的圓。
)處,順時針生成八分之一圓,利用對稱性畫出全部的圓。


為了套用中點畫圓法,我們定義一個圓函式

任何點(x,y)的相對位置可由圓函式的符號來檢測:
F(x,y) | <0 點(x,y)位於數學圓內 =0 點(x,y)位於數學圓上 >0 點(x,y)位於數學圓外 |
算法演示
如下圖所示,圖中有兩條圓弧A和B,假定當前取點為Pi(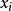 ,
,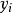 ),如果順時針生成圓,那么下一點只能取正右方的點E(
),如果順時針生成圓,那么下一點只能取正右方的點E(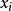 +1,
+1,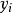 )或右下方的點SE(
)或右下方的點SE(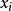 +1,
+1,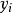 -1)兩者之一。
-1)兩者之一。
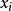
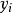
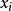
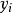
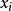
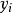
假設M是E和SE的中點,即,則:
1、對圓A來說,F(M)<0,M在圓A內,這說明點E距離圓更近,應取點E作為下一象素點;
2、對圓B來說,當F(M)>0,M在圓B外,表明SE點離圓更近,應取SE點為下一象素點;
3、而當F(M)=0時,在E點與SE點之中隨便取一個即可,我們約定取SE點。
2、對圓B來說,當F(M)>0,M在圓B外,表明SE點離圓更近,應取SE點為下一象素點;
3、而當F(M)=0時,在E點與SE點之中隨便取一個即可,我們約定取SE點。
實現過程
我們用中點M的圓函式作為決策變數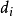 ,同時用增量法來疊代計算下一個中點M的決策變數
,同時用增量法來疊代計算下一個中點M的決策變數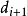 。
。
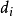
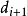
下面分兩種情況來討論在疊代計算中決策變數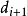 的推導。
的推導。
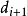
1、見圖①,若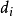 <0,則選擇E點,接著下一個中點就是,這時新的決策變數為:
<0,則選擇E點,接著下一個中點就是,這時新的決策變數為:
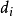
<img title="①(di
由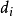 和
和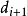 的表達式推出
的表達式推出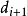 =
=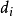 +2
+2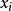 +3
+3
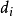
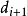
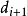
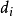
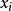
2、見圖②,若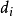 ≥0,則選擇SE點,接著下一個中點就是,這時新的決策變數為:
≥0,則選擇SE點,接著下一個中點就是,這時新的決策變數為:
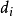
由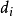 和
和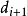 的表達式推出
的表達式推出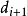 =
=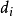 +2(
+2(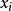 -
-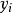 ) +5
) +5
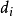
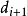
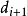
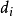
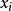
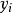
我們利用遞推疊代計算這八分之一圓弧上的每個點,每次疊代需要兩步處理:
(1)用前一次疊代算出的決策變數的正負來決定本次選擇的點
(2)對本次選擇的點,遞推計算得出新的決策變數的值
接下來只要計算出初始決策變數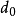 即可,對於初始坐標(0,R),顯然順時針生成的下一個點的坐標是(1,
即可,對於初始坐標(0,R),顯然順時針生成的下一個點的坐標是(1, )
)
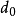

算法偽代碼
1、輸入:圓半徑r、圓心(x0,y0);
2、確定初值:x=0,y=r、d=5/4-r;
3、While(x<=y){
利用八分對稱性,用規定的顏色color畫八個象素點(x,y);
if(d≥0){
2、確定初值:x=0,y=r、d=5/4-r;
3、While(x<=y){
利用八分對稱性,用規定的顏色color畫八個象素點(x,y);
if(d≥0){
x=x+1;
y=y-1;
d=d+2(x-y)+5;
}
else
y=y-1;
d=d+2(x-y)+5;
}
else
x = x+1;
d=d+2x+3;
}
d=d+2x+3;
}

