中心仿射變換群是仿射變換群的子群,即平面上以同一點為中心的中心仿射變換的全體構成一個群,稱為中心仿射變換群。
基本介紹
- 中文名:中心仿射變換群
- 所屬學科:數學
- 所屬問題:高等幾何(仿射幾何)
- 相關概念:中心仿射變換
基本介紹
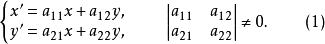

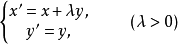
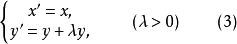
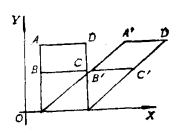 圖1
圖1中心仿射群
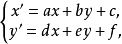

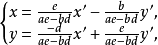
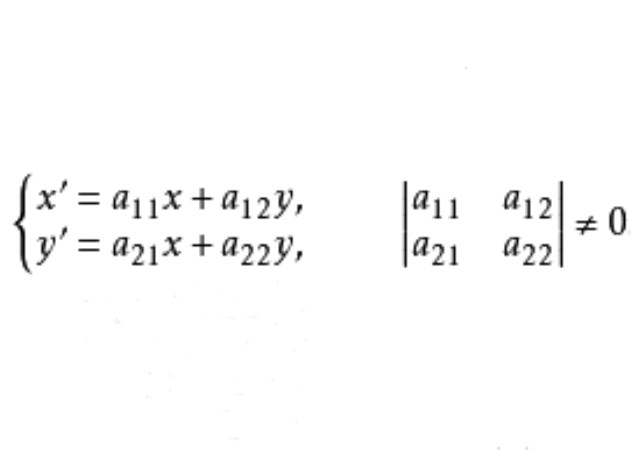
中心仿射變換群是仿射變換群的子群,即平面上以同一點為中心的中心仿射變換的全體構成一個群,稱為中心仿射變換群。
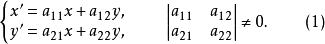

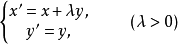
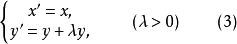
 圖1
圖1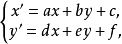

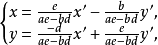
中心仿射變換群是仿射變換群的子群,即平面上以同一點為中心的中心仿射變換的全體構成一個群,稱為中心仿射變換群。...
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。仿射變換群是指仿射空間A的所有自同構組成A的置換群的子群,稱為A的...
中心仿射變換(central affine transformation)是一類重要的仿射變換,指含一個不變點的仿射變換。位似變換是中心仿射變換的特例。...
則稱G為S的一個變換群。例如,平面上正交變換的全體構成的變換群稱為正交群;平面上仿射變換的全體構成的變換群稱為仿射群。平面上射影變換的全體構成的變換群稱為...
簡稱相似群。是一類基本的變換群。平面上所有相似變換的集合構成群,稱為相似變換群。它是一個四維群。仿射變換群的子群。在仿射變換中若保持一對點I(1,i,0),...
仿射等價(affine equivalence)是圖形間的一種等價關係。若存在一個仿射變換把圖形C1變成C2,則稱C1與C2仿射等價。否則稱為仿射不等價。圖形的仿射等價是一種等價關係...
仿射變換是射影變換的特殊情況,當定義中心射影的線束為互相平行的直線時,變換稱為仿射變換,由於線束中的直線互相平行,顯然,仿射變換保持交比不變。[2] ...
在射影平面(或射影空間)中指定一條(或一個)直線l(或超平面π),那么射影變換群中保持l(或π)不動的變換就構成一個與仿射變換群同構的變換子群。從這個意義...
仿射微分幾何學(affine ldifferential geometry)是一門古典的微分幾何,屬於微分幾何學的一個分支,從屬於仿射變換群。內容包括曲線和曲面在仿射變換群下的不變數、協...
