中國學者於20世紀50年代提出的一種典型的組合最佳化問題，後在國際上被稱為中國郵路問題(Chinese postman problem)。已知圖G=(V，E)，對於每條邊e∈E，有距離d(e)，從G的某節點出發，走過G的所有邊(允許重複穿過)，回到原出發點，使其總行程最短，這個問題是P問題。
基本介紹
- 中文名：中國郵路問題
- 外文名：Chinese postman problem
- 相關人物：管梅谷
- 所屬學科：數學
- 所屬問題：運籌學(組合最最佳化)
基本介紹,問題的解答,
基本介紹
一個郵遞員送信，要走完他負責投遞的全部街道，完成任務後回到郵局，應按怎樣的路線走，他所走的路程才會最短呢?如果將這個問題抽象成圖論的語言，就是給定一個連通圖，連通圖的每條邊的權值為對應的街道的長度(距離)，要在圖中求一迴路，使得迴路的總權值最小。顯然，若圖為歐拉圖，只要求出圖中的一條歐拉迴路即可。否則，郵遞員要完成任務就得在某些街道上重複走若干次。如果重複走一次，就加一條平行邊，於是原來對應的圖就變成了多重圖。只是要求加進的平行邊的總權值最小就行了。於是問題就轉化為：在一個有奇度數結點的賦權連通圖中，增加一些平行邊，使得新圖不含奇度數結點，並且增加的邊的總權值最小。
問題的解答
要解決上述問題，應分下面兩大步驟。首先，增加一些邊，使得新圖無奇度數結點，稱這一步為可行方案：其次，調整可行方案，使其達到增加的邊的總權值最小，稱這個最後的方案為最佳方案。
【例1】 在圖1中，確定一條從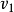
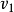到 的迴路，使它的權值最小。事實上，所確定的迴路從任何一個結點出發都可以。
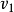
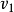
圖1（a）
圖1（b）
圖1（c）(1)一個可行方案的確定。
由於圖中奇度結點為偶數個，所以圖中奇度數結點可以配對。又由於圖的連通性，每對奇度數結點之間均存在基本通路，在配好對的奇度數結點之間各確定一條基本通路，然後將通路中的所有邊均加一條平行邊，這樣產生的新圖中無奇度數結點，因而存在歐拉迴路。在圖1(a)中，奇度數結點有4個：
。任意將它們配2對：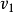
與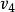
配對，v3與v6配對，選v1與v4之間的基本通路為
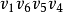，v3與v6之間的基本通路為
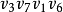。每條通路中所含的邊均加一條平行邊。增加平行邊後如圖1(b)所示，它無奇度數結點，因而是歐拉圖。增加的邊的總權值為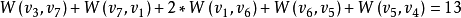
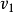
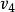
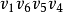
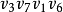
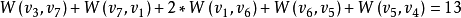
(2)調整可行方案，使增加的邊的總數減少。
圖1(b)中，邊
的重數為3，若去掉兩條邊，既不影響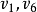
度數的奇偶性，也不影響圖的連通性，因而可去掉兩條邊。一般情況下，若邊的重數大於等於3，就去掉偶數條邊。於是有下面結論：
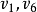
①在最優方案中，圖中每條邊的重數小於等於2。
經分析發現，如果將某條基本迴路中的平行邊均去掉，而給原來沒有平行邊的邊加上平行邊，不影響圖中結點度數的奇偶性。因此，如果在某條基本迴路中，平行邊的總權值大於該迴路的權值的一半，就作上述凋整。在圖(b)中，迴路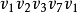
的權值為6，而平行邊的總權值為4，大於3，因而應給予調整，調整後如圖(c)所示。故得到下面的結論：
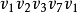
②在最優方案中，圖中每個基本迴路上平行邊的總權值不大於該迴路的權值的一半。
經過以上調整，得圖1(c)，平行邊的總權值為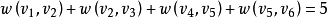
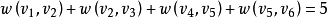
(3)判斷最佳方案的標準。
從上面的分析中可知，一個最佳方案是滿足①、②的可行方案，反之， 個可行方案若滿足①、②兩條，也一定是最佳方案。因而①、②是最佳方案的充分必要條件。
圖1(c)滿足①、②兩條，從而是最佳方案，即圖中的任意一條歐拉迴路均為郵遞員的最佳送信路線。
檢查是否滿足條件②，就要檢查所有的基本迴路，工作量很大，但這個問題已有了較好的算法了，這裡不作介紹。
上述問題是由我國數學家管梅谷在1962年首先解決的，在國際上稱為郵路問題。
