基本介紹
- 中文名:不變環面吸引子
- 外文名:invariant torus attractor
- 別名:擬周期吸引子
- 所屬學科:數學
- 所屬領域:系統理論(動態系統)
基本介紹,吸引子及其功率譜,
基本介紹
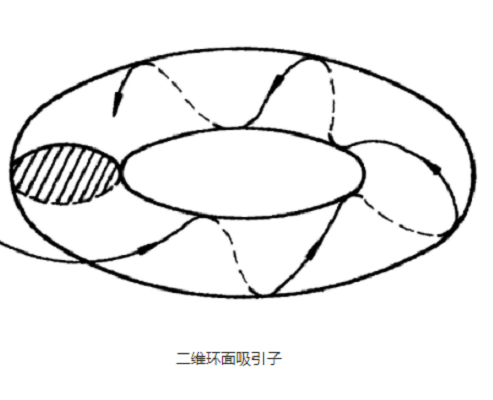
不變環面(擬周期)吸引子表現為一個封閉的環面,描述複合振盪的擬(準)周期行為,它的軌道在相空間中的一個環面上繞行,而且永不重複永不相交。當 為無理數時,在環面與平面上的軌道都充滿整個環面和平面,這時形成了擬周期吸引子。
為無理數時,在環面與平面上的軌道都充滿整個環面和平面,這時形成了擬周期吸引子。

吸引子(attractor)是相空間的一種特殊點集。在耗散動態系統中,狀態隨時間演化若可無限趨近於某低維或有限吸收集上,則該吸收集稱為吸引子。常見的吸引子有諸如:點(定常狀態)吸引子、極限環(周期狀態)吸引子、不變環面(擬周期狀態)吸引子和奇怪(混沌)吸引子等,沿時間增長正向演化的吸引子亦稱ω吸引子,而沿時間減少反向演化的則稱α吸引子。
吸引子及其功率譜

其中 則
則 。
。


(1)式表明,相軌跡最後被吸引到一個有限的子相空間中去。該子相空間就是吸引子,也就是最終都會趨向於某種穩定態,這種穩定態在相空間裡是由點(某一狀態)或點的集合(某種狀態序列)來表示的。這種點或點的集合對周圍的軌道似乎有種吸引作用,從附近出發的任何點都要趨近於它;系統的運動也只有到這個點或點集上才穩定下來並保持下去。它表示著這系統的穩定態是動力系統的最終歸宿;即系統行為最終被吸引到的子相空間處所。經典力學指出,有三種類型的吸引子:一種是穩定的不動點,它代表一個穩定態,叫定常吸引子,如二維相空間中的穩定結點和焦點。第二種是穩定的“極限環”,即相空間中的封閉軌線,在它外邊的軌線都向里卷,在它裡邊的軌線都向外伸,都以這個封閉曲線為其極限狀態。極限環代表一種穩定的周期運動,因此,也叫周期吸引子。第三類吸引子是穩定的環面,代表系統的準周期運動,也叫擬周期吸引子。周期吸引子和擬周期吸引子,在其環面上有兩個運動方向的頻率 和
和 如果
如果 為有理數時,就會形成周期吸引子;如果
為有理數時,就會形成周期吸引子;如果 為無理數時,則就形成擬周期吸引子。上述三類吸引子,都代表規則的有序運動,所以只能用於描述經典動力力學,而不能描述混沌運動。有耗散的非線性系統的長期行為也可能要穩定在相空間的一個低維的點集合上,這些點集合也是一種吸引子,但是它絕不可能最終達到規則的有序運動。這是因為一方面相空間體積不斷的收縮,另一方面非線性系統的內部隨機性、非線性性使它不斷的演化,因而在它的吸引子內部,運動也是極不穩定的,在這種吸引子上,系統的行為呈現典型的隨機性、活躍易變、極不確定,因而它的幾何圖像極其複雜,所以茹勒和泰肯斯把他們稱為“奇怪吸引子”或“混沌吸引子”,以區別前述那幾種“平庸吸引子”。這四種吸引子的重要特徵有:①穩定性。當一個小的擾動使系統暫時偏離吸引子後,它必然會再返回來。②低維性。它作為相空間的點集合,其維數必定小於相空間的維數。然而奇怪吸引子,還具有一個突出的新特點,即非周期性它永遠不會自相重複,永遠不會自交或相交。因此,奇怪吸引子的軌跡將會在有限區域內具有無限長的長度。研究還表明,混沌吸引子往往具有非整數維數。在耗散系統中,往往有多個吸引子並存,通常把吸引某個吸引子的點集叫該吸引子的吸引盆。如兩個鞍點之間的連線吸引盆叫分型線(即有界振動和無界旋轉區的分界線)。
為無理數時,則就形成擬周期吸引子。上述三類吸引子,都代表規則的有序運動,所以只能用於描述經典動力力學,而不能描述混沌運動。有耗散的非線性系統的長期行為也可能要穩定在相空間的一個低維的點集合上,這些點集合也是一種吸引子,但是它絕不可能最終達到規則的有序運動。這是因為一方面相空間體積不斷的收縮,另一方面非線性系統的內部隨機性、非線性性使它不斷的演化,因而在它的吸引子內部,運動也是極不穩定的,在這種吸引子上,系統的行為呈現典型的隨機性、活躍易變、極不確定,因而它的幾何圖像極其複雜,所以茹勒和泰肯斯把他們稱為“奇怪吸引子”或“混沌吸引子”,以區別前述那幾種“平庸吸引子”。這四種吸引子的重要特徵有:①穩定性。當一個小的擾動使系統暫時偏離吸引子後,它必然會再返回來。②低維性。它作為相空間的點集合,其維數必定小於相空間的維數。然而奇怪吸引子,還具有一個突出的新特點,即非周期性它永遠不會自相重複,永遠不會自交或相交。因此,奇怪吸引子的軌跡將會在有限區域內具有無限長的長度。研究還表明,混沌吸引子往往具有非整數維數。在耗散系統中,往往有多個吸引子並存,通常把吸引某個吸引子的點集叫該吸引子的吸引盆。如兩個鞍點之間的連線吸引盆叫分型線(即有界振動和無界旋轉區的分界線)。




對於吸引子的刻畫一般地在“巨觀”與“微觀”這兩個層次上進行。所謂“巨觀”刻畫是指使用對整個吸引子或無窮長的軌道平均後得到的特徵量,例如李雅普諾夫指數、功率譜分析、維和熵等,而“微觀”刻畫是指構成混沌吸引子的骨架的不穩定周期的數目、種類和它們的本徵值。自20 世紀80 年代中期以來,這兩方面的工作都形成了一套理論框架和方法,也都發展了從實驗數據中提取有關信息的技術。這四種吸引子所關切的主要問題是運動軌道的回歸行為,即演化過程回歸到曾經有過的狀態附近。一般說來,人類只能關心回歸行為,從以往的經歷預測未來。“歷史的螺旋式上升”,“似曾相識燕歸來”都是回歸行為。回歸行為中必包含一切可能的頻率成分或頻率結構,這不僅僅是數學,而且離不開物理考慮。我們從功率譜分析中,研究吸引子的運動狀態及信息序列。因此,功率譜中的寬頻,被作為可能存在混沌的簡單指示。特別是功率譜中的尖峰和寬頻背景,作為區分周期與噪聲的主要手段。






然後計算 即第k個頻率分量對
即第k個頻率分量對 的貢獻就等於兩傅立葉係數的平方和,這在物理上是十分明顯的(一個簡諧的功率與振幅的平方成正比)。另外時間序列中,包含兩個“時間常數”,即採樣間隔
的貢獻就等於兩傅立葉係數的平方和,這在物理上是十分明顯的(一個簡諧的功率與振幅的平方成正比)。另外時間序列中,包含兩個“時間常數”,即採樣間隔 和總採樣時間
和總採樣時間 。這兩個常數的倒數,決定了兩個特徵頻率
。這兩個常數的倒數,決定了兩個特徵頻率







通過時間序列分析非線性動力系統的波動狀態,不難從功率譜上區分周期函式、擬周期函式和非周期函式,從而也就分析了四種吸引子的功率譜特徵。
(i) 周期吸引子:它的功率譜是分立的、離散的(對應的尖峰),包括基頻 (T為時間序列的周期)和諧波
(T為時間序列的周期)和諧波 或分頻
或分頻 如圖1所示。
如圖1所示。



(ii) 擬周期吸引子:它包含各種各樣的周期(或頻率),且各頻率之比為無理數。如含有兩個頻率 和
和 的擬周期函式,它不僅包含原有的頻率
的擬周期函式,它不僅包含原有的頻率 和
和 ,由於非線性相互作用,還產生新的頻率,
,由於非線性相互作用,還產生新的頻率, (m,n 為任何整數,如
(m,n 為任何整數,如 )因此,擬周期吸引子的功率譜雖然也是分立的、離散的,但並不像周期吸引子那樣以某間隔的頻率分立,如圖2所示。
)因此,擬周期吸引子的功率譜雖然也是分立的、離散的,但並不像周期吸引子那樣以某間隔的頻率分立,如圖2所示。






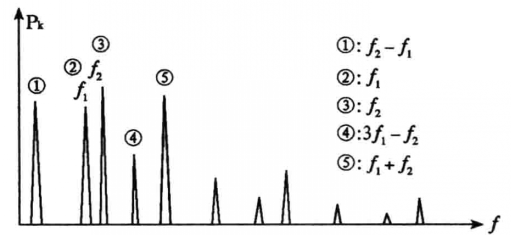 圖2 擬周期函式的功率譜
圖2 擬周期函式的功率譜(iii )奇怪吸引子:由於它具有非周期性,就會出現一批對應新分頻及倍頻的峰。因此功率譜是連續的但是不光滑,會在譜中出現噪聲背景及寬峰,如圖3所示。
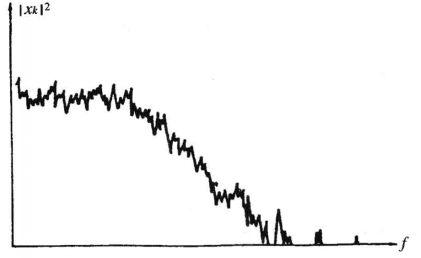 圖3 混沌的功率譜
圖3 混沌的功率譜