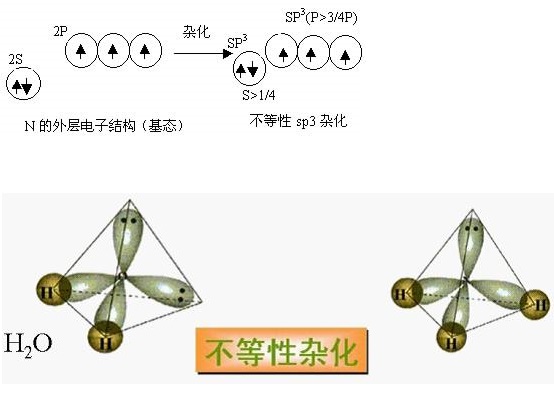
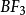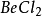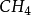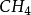雜化軌道可分為等性雜化和不等性雜化兩種。不等性雜化指參加雜化的各原子軌道中所含的未成對電子數不相等,雜化後所生成的雜化軌道的形狀和能量不完全等同,或者說在每個雜化軌道中所含s成分和p成分的比例不完全相等。
基本介紹
- 中文名:不等性雜化
- 外文名:nonequivalent hybridization
- 屬性:雜化方式
- 所屬學科:化學
簡介,定義,舉例,不等性雜化形成,等性雜化,定義,舉例,
簡介
雜化軌道理論是為了解釋多原子分子的空間構型問題,於1931年由鮑林和斯萊脫根據電子具有波性,波可以互相疊加的量子力學原理,在價鍵理論的基礎上建立起來的。該理論不僅成功地解釋了許多分子的幾何構型,而且還加深了人們對分子構型的理解。它既直觀, 又易於接受, 所以, 在《無機化學》分子結構一章中將該理論作為重點介紹的內容。
不等性雜化的特點是參加雜化的各原子軌道中所含的未成對電子數不相等,雜化後所生成的各雜化軌道的形狀和能量不完全等同。或者說每個雜化軌道中所含s成分和p成分的比例不相等,這類雜化叫做不等性雜化。
定義
在雜化過程中形成的各新雜化軌道所含s 和 p 的成分不相等,這樣的雜化稱為不 等性雜化,形成的雜化軌道為不等性雜化軌道。
舉例
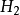
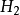
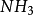
 氨氣分子雜化過程
氨氣分子雜化過程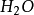
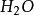
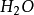
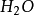
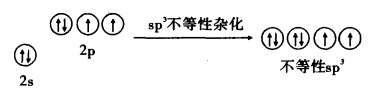 水分子雜化過程
水分子雜化過程
不等性雜化形成
眾所周知,將同一個原子的若干不同類型的原子軌道“ 混合” 起來, 重新組成一組新原子軌道的過程叫原子軌道的雜化,而形成的一組新軌道叫雜化軌道。當形成的一組雜化軌道完全等同(成分相等,能量相同時,這種雜化又叫等性雜化,否則為不等性雜化。對於這一點,各種教科書中的說法是相一致的。但是,對於如何引起雜化軌道中成分不等而形成不等性雜化卻各有評說。
第一種觀點認為:凡是由於雜化軌道中有不參加成鍵的孤電子對的存在,而形成不完全等同的雜化軌道,這種雜化叫不等性雜化。這也是多種《無機化學》教科書上較普遍的說法。
第二種觀點則認為:對於不等性雜化,不僅要考慮中心原子是否有孤對電子,而且還要考察與中心原子相互作用的其它原子的影響。若中心原子A 與完全相同的原子或基團B形成共價鍵,由於所形成的鍵都一樣,A 原子軌道一般採取等性雜化,若中心原子A 與不相同的其它原子或基團B和C同時結合,就會形成不同的鍵而出現不等性雜化。
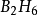
第四種觀點認為:不等性雜化又分為有孤對電子參加的雜化和沒有孤對電子參加的雜化(又叫部分雜化)兩種類型。所謂部分雜化是指中心原子成鍵的原子軌道只有一部分原子軌道參加雜化,且生成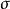 鍵,而未雜化的原子軌道形成π鍵。
鍵,而未雜化的原子軌道形成π鍵。
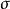
等性雜化
定義
在雜化過程中形成的每一種雜化軌道所含的s 及 p 的 成分相等, 這樣的雜化稱為等性雜化,形成的雜化軌道為等性雜化軌道。
舉例
如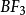 、
、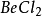 、
、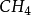 等分子為等性雜化。基 態 Be的外層電子構型為2s2,在成鍵時先發生激發,成為激發態2s12p1。隨即發生雜化,即Be的1個2s 軌道和1個2p軌道進行sp雜化,形成兩個sp雜化軌道,每個雜化 軌道中各有一個未成對電子。兩個C1原子的3p1軌道以“頭頂頭”方式與各雜化軌道大的一端重疊,形成兩個σ鍵。由於Be的兩個sp雜化軌道間的夾角是180°,因此所形成的 BeCI2的幾何構型為直線形。基態C原子只有兩個未成對電子,在形成
等分子為等性雜化。基 態 Be的外層電子構型為2s2,在成鍵時先發生激發,成為激發態2s12p1。隨即發生雜化,即Be的1個2s 軌道和1個2p軌道進行sp雜化,形成兩個sp雜化軌道,每個雜化 軌道中各有一個未成對電子。兩個C1原子的3p1軌道以“頭頂頭”方式與各雜化軌道大的一端重疊,形成兩個σ鍵。由於Be的兩個sp雜化軌道間的夾角是180°,因此所形成的 BeCI2的幾何構型為直線形。基態C原子只有兩個未成對電子,在形成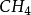 時 ,在H的影響下,C的1個2S軌道和3個2p軌道進行sp3雜化,形成4個sp3雜化軌道,每個Sp3雜化軌道中各有一個未成對電子。C用4個Sp3雜化軌道分別與4個H的1s軌道重疊形成4個σ鍵。由於C的4個sp3雜化軌道間的夾角為109°28',所以生成的
時 ,在H的影響下,C的1個2S軌道和3個2p軌道進行sp3雜化,形成4個sp3雜化軌道,每個Sp3雜化軌道中各有一個未成對電子。C用4個Sp3雜化軌道分別與4個H的1s軌道重疊形成4個σ鍵。由於C的4個sp3雜化軌道間的夾角為109°28',所以生成的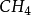 的幾何構型為正四面體。
的幾何構型為正四面體。