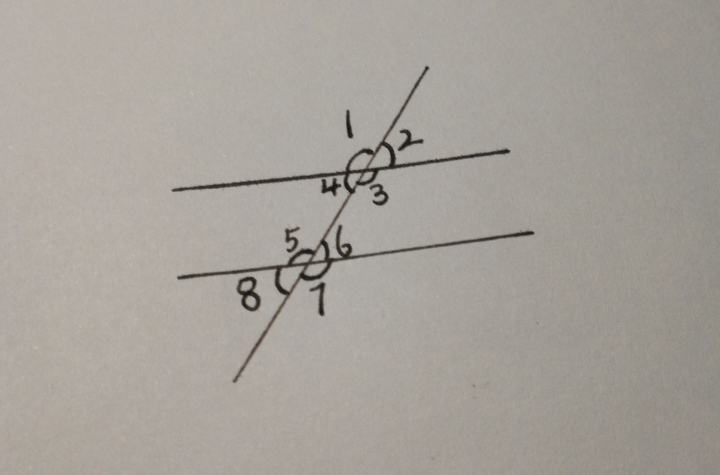
基本介紹
- 中文名:三線八角
- 外文名:Three Lines and Eight Angles
- 所屬學科:數學
- 所屬問題:平面幾何
- 簡介:兩條直線被第三條直線所截
定義,八個角的相對位置,
定義
在同一平面內,兩條直線被一條直線相截所形成的八個角稱為“三線八角”。
八個角的相對位置
兩條直線被第三條直線所截,所得的八個角,叫做三線八角。如圖1所示:圖中的: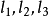 和∠1、∠2、∠3、∠4、∠5、∠6、∠7、∠8就是三線八角。按上述八個角的相互位置,給以下列不同名稱:
和∠1、∠2、∠3、∠4、∠5、∠6、∠7、∠8就是三線八角。按上述八個角的相互位置,給以下列不同名稱:
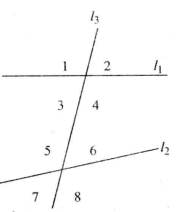 圖1
圖1①同位角:當形成三線八角時,如果有兩個角分別在兩條直線的同一方,並且在第三條直線的同一旁,這樣的一對角,叫做同位角。
如圖中的∠1與∠5、∠2與∠6、∠4與∠8、∠3與∠7都是同位角。
②內錯角:如果兩個角都在兩直線的內側,並且在第三條直線的兩側,那么這樣的一對角叫做內錯角。
如圖中的∠6與∠3、∠4與∠5都是內錯角。
③外錯角:如果兩個角都在兩直線的外側,並且在第三條直線的兩側,那么這樣的一對角叫做外錯角。
如圖中的∠1與∠8、∠2與∠7都是外錯角。
④同旁內角:如果有兩個角都在兩條直線的內側,並且在第三條直線的同旁,那么這樣的一對角,叫做同旁內角。
如圖中的∠3與∠5、∠4與∠6都是同旁內角。
⑤同旁外角:如果有兩個角都在兩條直線的外側,並且在第三條直線的同旁,那么這樣的一對角,叫做同旁外角。
如圖中的∠1與∠7,∠2與∠8都是同旁外角。
注意事項:
同位角、內錯角等是成對出現的,不能說“∠5是內錯角”、“∠6是同旁內角”等。不可將三個角的名稱混淆!