基本介紹
- 中文名:三段論公理
- 外文名:axioms of syllogism
- 所屬學科:邏輯學
- 性質:與推理有關的一個公理
- 簡介:直言三段論推理的根據
基本內容
三段論公理的圖形表示

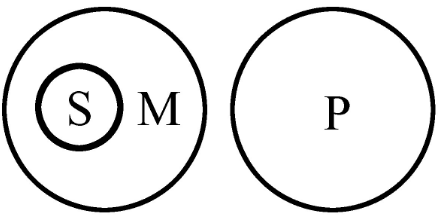
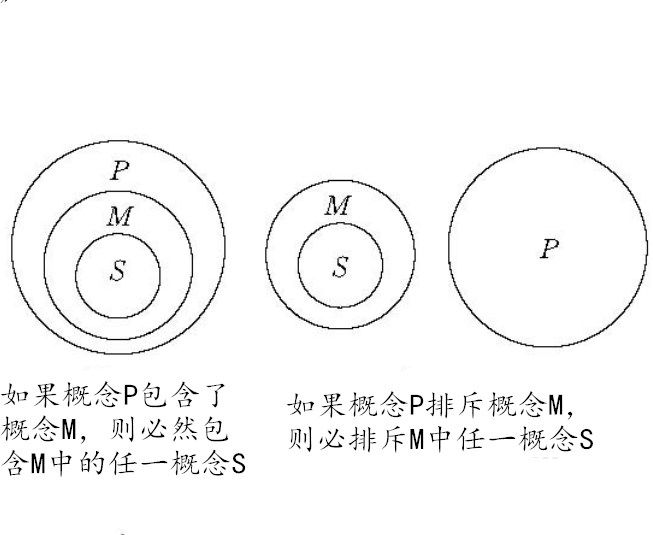


三段論公理(axioms of syllogism)是與推理有關的一個公理,是直言三段論推理的根據。公理為:凡對一類事物的全部對象有所肯定(或否定),則對該類事物的任一對象也必然有所肯定(或否定)。這一公理在三段論推理中...
人們根據三段論公理,總結出三段論的一般推理規則,使之成為判定三段論是否有效的標準。三段論的一般規則共有七條,其中前四條是基本規則,後三條是導出規則。在這七條規則中,前三條是關於詞項的規則;後四條是關於前提與結論的規則。一般規則如下:(1)一個正確的三段論,有並且只有三個不同的項。三段論的實質就...
三段論的上述規則,是三段論公理所反映的客觀規律性在三段論形式中的體現和具體化。這些規則有些是基本的(如前五條),有些則是由其他規則所推導出來的(如後二條)。但它們都統一地保證著三段論形式的有效性,從而遵守這些規則,就能由真的前提必然地推出真的結論。而違反其中任何一條規則,就不是一個正確的、有效的...
公理化方法發展的第一階段是由亞里士多德的完全三段論到歐幾里得《幾何原本》的問世.大約在公元前3世紀,希臘哲學家和邏輯學家亞里士多德總結了幾何學與邏輯學的豐富資料,系統地研究了三段論,以數學及其它演繹的學科為例,把完全三段論作為公理,由此推導出其它所有三段論法,從而使整個三段論體系成為一個公理系統.因此...
三段論化歸法亦稱“三段論的還原法”。將三段論的第二、三、四格轉化為第一格的方法。從整體上看,三段論是一個完整的公理演繹系統,它的第一格為“完善格”,其中的AAA和EAE式是公理的典型體現。因此,三段論的所有有效式均可轉化為第一格。化歸的具體步驟是:①首先要確定變動的前提;②對需要變動的前提進行判斷...
P:,有些哺乳動物(S)是翼手目動物?M),所以,有些哺乳動物(S)是能飛翔的(P),”通過三段論的還原?可以把繁多的三段論形式從三毆診第一格的兩個基本形式即AAA式與EAE式推導出來。因此,可以把三段論第一格的AAA式與EAE式看作實質上是三段論整個體系的公理,而整個三段論體系也就可視作為一個完整的公理體系。
P:,有些哺乳動物(S)是翼手目動物?M),所以,有些哺乳動物(S)是能飛翔的(P),”通過三段論的還原?可以把繁多的三段論形式從三毆診第一格的兩個基本形式即AAA式與EAE式推導出來。因此,可以把三段論第一格的AAA式與EAE式看作實質上是三段論整個體系的公理,而整個三段論體系也就可視作為一個完整的公理體系。
經由可靠的論證(三段論、推理規則)由前提(原有的知識)導至結論(新的知識)的邏輯演繹方法,是由古希臘人發展出來的,並已成為了現代數學的核心原則。除了重言式之外,沒有任何事物可被推導,若沒有任何事物被假定的話。公理即是導出特定一套演繹知識的基本假設。公理不證自明,而所有其他的斷言(若談論的是...
P:,有些哺乳動物(S)是翼手目動物?M),所以,有些哺乳動物(S)是能飛翔的(P),”通過三段論的還原?可以把繁多的三段論形式從三毆診第一格的兩個基本形式即AAA式與EAE式推導出來。因此,可以把三段論第一格的AAA式與EAE式看作實質上是三段論整個體系的公理,而整個三段論體系也就可視作為一個完整的公理體系。
15、完全的和不完全的三段論 16、詞項邏輯與命題邏輯 17、換位法證明 18、歸謬法證明 19、顯示法證明 20、排斥的形式 21、一些未解決的問題 第四章用符號形式表達的亞里士多德系統 22、符號系統的說明 23、演繹理論 24、量詞 25、三段論系統的基本要素 26、三段論的斷定命題的推導 27、排斥的表達式的公理和規則 ...
三段論的公理 又稱曲全公理。直言三段論推理的依據。內容為:凡對一類事物有所肯定,則對該類事物中的每一個對象也有所肯定;凡對一類事物有所否定,則對該類事物中的每一個對象也有所否定。三段論的規則 要保證直言三優論推理的有效性,就必須遵守一定的規則。三段論的規則共二類四條。第一類是關於詞項的規則:(...
三段論的公理 又稱集合公理。直言三段論推理的依據。內容為:凡對一類事物有所肯定,則對該類事物中的每一個對象也有所肯定;凡對一類事物有所否定,則對該類事物中的每一個對象也有所否定。三段論的規則 要保證直言三段論推理的有效性,就必須遵守一定的規則。三段論的規則共二類四條。第一類是關於詞項的規則:(一...
他詳盡地探討了命題邏輯,系統地研究了直言三段論和假言三段論,同時還把亞里士多德的邏輯和斯多阿學派的邏輯結合在一起。他在亞里士多德的直言命題理論基礎上提出的“波愛修方陣”,即“邏輯方陣”,至今仍被採用。傳統邏輯所謂的三段論公理,也是由他確定的。古羅馬邏輯是中世紀邏輯研究的起點,它在邏輯理論的發展上...
曲全公論(英axiom of syllogism;拉 dictum de omniet nullo)“三段論公理”的舊譯。中國嚴復在其譯著《穆勒名學》一書中,首次用此譯名,並解釋說:“案悉舉日全,偏舉日曲。曲全公論首標於亞里斯大德(即”亞里士多德“),所謂全是全非公例是也。其例曰:於一普及之名而有所謂者,全正者曲亦正,全...
三段論的化歸 亞里士多德已充分討論過三段論的化歸問題,建立了人類歷史上最早的公理系統之一。他所開創的傳統邏輯利用對當關係、換質和換位、歸謬法等,把其他格的三段論化歸為第1格,並用Barbara證明第1格的其他各式,從而把24個有效的三段論形式組成一個公理系統。三段論的圖解 邏輯史上有許多不同的圖解方法,其中...
用下面4條公理:(一)Aaa (二)Iaa (三)Abc∧Aab→Aac (四)Abc∧Iba→IbC 其中第三條公理是三段論第一格的AAA式,第四條公理是第三格的AII式。再藉助代入規則、分離規則以及命題演算的規律,就可推出直言命題的換位規律和所有的三段論的有效式。這個完全形式化的三段論公理系統的建立使人們對傳統邏輯的三段論...
三段論的第一格典型地體現了演繹推理由一般到特殊的思維進程,它的AAA式和EAE式又直接體現了三段論的公理,並且在三段論的四個格中,只有第一格才能推出直言命題的四種形式:A、E、I、O,而且也只有第一格才能推出全稱肯定命題(A),故亞里士多德稱之為“完善的格”,傳統邏輯也稱之為“典型格”。三段論第一格在...
3. 直言三段論 3.1 三段論的構成 3.2 三段論公理 3.3 三段論規則 3.4 三段論的格與式 3.5 非標準形式的三段論 3.6 三段論的零式判別法 本章思考與練習 第七章 演繹推理(下)1. 聯言推理 1.1 聯言合成 1.2 聯言分解 2. 選言推理 2.1 相容選言推理 2.2 不相容選言推理 3. 假言推理 3.1 關於...
第三節 三段論 一、三段論的概述 二、三段論的公理 三、三段論的規則 四、三段論的格與式 五、三段論的省略式 六、安全生產與三段論 第四節 複合判斷及其推理與認識事故 一、複合判斷及其推理的基本概念 二、聯言判斷與聯言推理 三、選言判斷與選言推理 四、假言判斷與假言推理 第四章 歸納邏輯概述 第五章 歸納...
第四節 三段論 一、什麼是三段論 二、三段論公理 三、三段論的規則 四、三段論的格與式 五、三段論的省略式 第四章 關係命題及其推理 第一節 關係命題 一、什麼是關係命題 二、關係的邏輯性質 第二節 關係推理 一、什麼是關係推理 二、純關係推理 三、混合關係推理 第五章 複合命題及其推理 第一節 聯言命題...
第三節三段論 一、 什麼是三段論 二、 三段論的組成 三、 正確進行三段論推理的條件 四、 三段論的公理 五、 三段論推理的一般規則 六、 各格的特殊規則 七、 三段論的式 八、 三段論的省略式 第四節複合判斷推理 一、 聯言推理 二、 選言推理 三、 假言推理 四、 二難推理 第五節歸納推理和類比推理 一、...
第三節 三段論 一、三段論的概念 二、三段論的公理 三、三段論的規則 四、三段論的格和式 五、省略三段論 六、複合三段論、連鎖三段論、帶證式三段論 第四節 關係推理 一、關係推理的概念 二、純關係推理 第五節 小結 第七章 演繹推理二 第一節 聯青推理 一、聯言推理的定叉 二、分解式聯言推理 三、組合...
第四講 生活中的潛意識——三段論推理 一、規範行為的意識——什麼是三段論 二、先人之見的鞏固性——三段論的公理 三、大家分享的規則——三段論的規則 北京大學有幾千所——只能有三個概念 翠花是韓國人——中項在兩個前提中至少要周延一次 不成功就裸奔——前提中不周延的項,結論中不得周延 黃瓜不是西紅柿...
第四講 生活中的潛意識——三段論推理 一、規範行為的意識——什麼是三段論 二、先人之見的鞏固性——三段論的公理 三、大家分享的規則——三段論的規則 北京大學有幾千所——只能有三個概念 翠花是韓國人——中項在兩個前提中至少要周延一次 不成功就裸奔——前提中不周延的項,結論中不得周延 黃瓜不是西紅柿...
第一節 三段論推理 一、三段論的定義與結構 二、三段論的公理和規則 三、三段論的格和式 四、省略三段論及其復原 第二節 複合命題推理 一、聯言推理及套用 二、選言推理及套用 三、假言推理及套用 第三節 二難推理 一、二難推理的概念及特徵 二、二難推理的分類 三、二難推理在法律工作中的運用 第九章 歸納...
亞里士多德的模態三段論實質上是一個公理系統。他像處理實然三段論(見三段論)一樣,把模態三段論分為第1、第2和第3格,並把第1格的模態三段論看作完美的、不需要證明的,而且主要套用換位法和歸謬法,就可以從第 1格的模態三段論推出其他的模態三段論。亞里士多德的學生泰奧弗拉斯多也創造了一個不同的模態三段論...
第二節直言三段論 一、什麼是直言三段論 二、直言三段論公理 三、直言三段論的規則 四、直言三段論的格 五、三段論的簡化形式和複雜形式 六、三段論推理的實踐意義 練習題 第三節關係推理 一、關係推理概述 二、關係推理典型示例 練習題 第四節假言推理 一、什麼是假言推理 二、假言直言推理 三、純假言推理 四、...
第一節 三段論概述 第二節 三段論公理與規則 第三節 三段論的格與式 第四節 三段論的省略形式 第五節 複合三段論 拓展討論:三段論的邏輯美 關鍵術語提要 進一步閱讀指南 問題與思考 練習題 第五章 關係判斷及其推理 第六章 複合判斷及其推理(上)第七章 複合判斷及其推理(下)第八章 模態判斷及推理 第九章 ...
第四節 直言三段論 一、直言三段論的定義和結構 二、直言三段論的公理 三、直言三段論的規則 四、直言三段論的格與式 五、直言三段論的省略式 練習題 第五章 謂詞邏輯 第一節 原子命題的內部結構 一、謂詞邏輯的任務 二、謂詞和個體詞 三、量詞 四、命題形式及其解釋 第二節自然語言的謂詞表達式 一、直言命題的...
