基本介紹
- 中文名稱:一元五次方程
- 外文名稱:Quintic Equation
- 方程:ax^5+bx^4+cx^3+dx^2+ex+f=0
- 條件:a,b,c,d,e,f∈R,且a≠0
- 係數:a,b,c,d,e
- 常數:f
- 現有公式:天珩公式
- 類型:整式方程
- 領域:數學
方程的定義,方程標準型,解法,天珩公式,複數域內通用公式,
方程的定義
方程標準型
形如 的方程是一元五次方程的標準型。
的方程是一元五次方程的標準型。

解法
天珩公式
本公式判別法的缺點是僅可求解實係數的部分五次方程。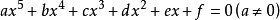 重根判別式:
重根判別式:
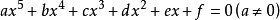

總判別式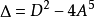
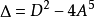
(1)若A=B=C=D=0,則方程有一個五重實根。

(2)若AD≠0,B=C=Δ=0,則方程有五個實根,其中有兩對二重根。
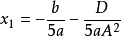

(3)若B=C=0,Δ>0,則方程有一個實根和兩對不等共軛虛根。
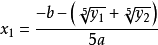


其中,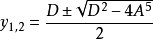
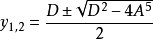
(4)若B=C=0,Δ<0,則方程有五個不等實根。



其中,

複數域內通用公式
先將方程配方:方程兩邊同時除以a,後令y=x+b/5a,即x=y-b/5a,化為關於y的一元五次方程:
y5+py3+qy2+ry+s=0
若滿足q=p2-5r=0,則方程可用以下方法求解:





其中,V是1的一個五次方根且不為1。可取 ,
,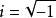

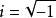
遇虛數開方時,可使用如下公式:



