μ律

μ律是PCM非均勻量化中的一種對數壓擴形式，數字脈衝編碼調製（PCM）是目前模擬信號數位化的基本方法，PCM包括採樣、量化、編碼三個步驟，其中量化是對抽樣值的取值離散，根據量化間隔的不同選取分為均勻量化和非均勻量化，非均勻量化可以有效地改善信號的量化信噪比。語音信號的量化常採用ITU建議的兩種對數形式的非均勻量化壓縮特性：A律和μ律，μ律編碼主要用於24路一次群系統，μ律PCM用於北美和日本。

基本介紹

• 中文名：μ律
• 外文名：μ-law
• 定義：壓擴標準
• 套用學科：通信科技（一級學科）等

概述

A律是ITU-T（國際電聯電信標準局）CCITT G.712定義的關於脈衝編碼的一種壓縮/解壓縮算法，北美和日本採用μ律PCM。μ律是PCM非均勻量化中的一種對數壓擴形式，脈衝編碼調製PCM是對一個時間連續的模擬信號先抽樣，再對樣值幅度量化，編碼的過程其中量化，就是把經過抽樣得到的瞬時值將其幅度離散，即用一組規定的電平，把瞬時抽樣值用最接近的電平值來表示,通常是用二進制表示。而量化中會出現誤差，即量化後的信號和抽樣信號的差值，量化誤差在接收端表現為噪聲，稱為量化噪聲。 量化級數越多誤差越小，相應的二進制碼位數越多，要求傳輸速率越高，頻帶越寬。 為使量化噪聲儘可能小而所需碼位數又不太多，通常採用非均勻量化的方法進行量化。非均勻量化根據幅度的不同區間來確定量化間隔，幅度小的區間量化間隔取得小，幅度大的區間量化間隔取得大。

常用的壓擴方法是對數型的A壓縮律和μ壓縮律。

圖1.是μ律壓縮特性曲線，其中為歸一化的量化器輸入，為歸一化的量化器輸出。常數愈大，則小信號的壓擴效益愈高，多採用u=255。律壓縮特性曲線如圖1所示。

μ律255/15折線

2.1 過程

μ律壓縮曲線是連續曲線。μ值不同，壓縮特性也不同。要設計電路來實現這樣的函式是相當複雜的；而且採用非線性量化法時，要用壓縮規律所規定的判定值直接和信號相比較，以確定信號所在量化級並直接作相應編碼，那是不容易的。為了使所需數字電路容易實現，就要求相鄰的判定值或量化間隔能成簡單的整數比(通常為2倍比)，而這一要求用平滑和連續變化的非均勻量化律是不容易滿足的。但如果採用若干段折線組成的非均勻量化壓縮律就很容易實現。因此，就發展了用折線逼近μ律和A律非均勻量化折線壓縮方式。

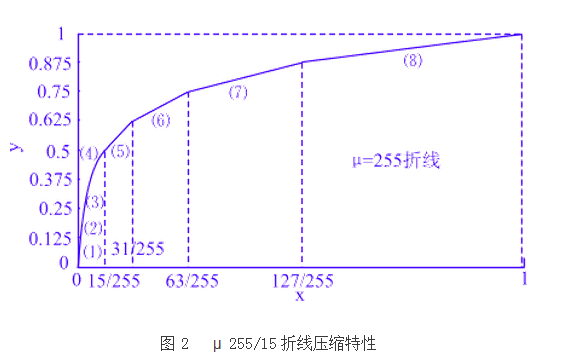
255/15μ律折線壓縮方式是將律曲線分16段做弦，當相鄰折線段的段距比值為2時，可以很好地逼近μ=255的μ律壓縮曲線的特性。實際上由於在原點兩側的第一條折線都通過原點，斜率相同而對稱，所以合成了一條折線，因而實際上總共只有15條折線。因此，這種折線壓縮律就稱為μ255/15折線壓縮律，如圖2所示。

表1列出了μ律 255/15折線的分段坐標值和各段斜率。

折線端		1	2	3	4	5	6	7	8
x	0	1/255	3/255	7/255	15/255	31/255	63/255	127/255	1
y; (μ-255/15）折線	0	1/8	2/8	3/8	4/8	5/8	6/8	7/8	1
折線斜率	32	16	8	4	2	1	1/2	1/4

表1 　μ255/15折線的分段坐標值和各段斜率

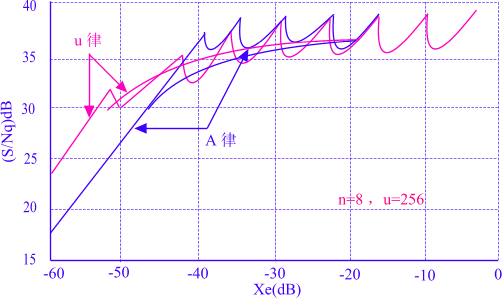
2.2 A律13折線量化信噪比的比較

採用A律13折線時的量化信噪比曲線的基本特徵與μ律相仿，如圖5所示，但採用μ律15折線編碼可以明顯提高小信號的信噪比，而且總的來看μ律的動態範圍要比A律的大一些，此處不再做定量討論。