實像虛像
在光學中,由實際光線匯聚成的像,稱為實像,能用光屏承接;反之,則稱為虛像,只能由眼睛感覺。有經驗的物理老師,在講述實像和虛像的區別時,往往會提到這樣一種區分方法:“實像都是倒立的,而虛像都是正立的。”所謂“正立”和“倒立”,當然是相對於原物體而言。
平面鏡、凸面鏡和凹透鏡所成的三種虛像,都是正立的;而凹面鏡和凸透鏡所成的實像,以及
小孔成像中所成的實像,無一例外都是倒立的。當然,凹面鏡和凸透鏡也可以成虛像,而它們所成的兩種虛像,同樣是正立的狀態。
那么人類的眼睛所成的像,是實像還是虛像呢?我們知道,人眼的結構相當於一個凸透鏡,那么外界物體在視網膜上所成的像,一定是實像。根據上面的經驗規律,視網膜上的物像似乎應該是倒立的。可是我們平常看見的任何物體,明明是正立的啊?這個與“經驗規律”發生衝突的問題,實際上涉及到大腦皮層的調整作用以及生活經驗的影響。
當物體與凸透鏡的距離大於透鏡的一倍
焦距小於二倍焦距時,物體成倒立的像,當物體從較遠處向透鏡靠近時,像逐漸變大,像到透鏡的距離也逐漸變長;當物體與透鏡的距離小於焦距時,物體成放大的像,是虛像。
當物體與凸透鏡的距離大於二倍焦距時,物體成倒立的像,這個像是蠟燭射向凸透鏡的光經過凸透鏡會聚而成的,是實際光線的會聚點,能用光屏承接,是實像。當物體與透鏡的距離小於焦距時,物體成正立的虛像。
凸透鏡
凸透鏡成像規律
(1)
一倍焦距以內,正立放大虛像;
成實像物和像在凸透鏡異側,成虛像在凸透鏡同側。
(2)
一倍焦距分虛實(和正倒)
兩倍焦距分大小
物近像遠像變大
物遠像近像變小。
但一倍焦距內,物遠像遠像變大。
物體到透鏡的距離u
| 像的大小
| 像的正倒
| 像的虛實
| 像的位置
| 像到透鏡的距離v
| 套用實例
|
u>2f
| 縮小
| 倒立
| 實像
| 與物異側
| 2f>v>f
| 照相機
|
u=2f
| 等大
| 倒立
| 實像
| 與物異側
| v=2f
| 特點:大小分界點 |
2f>u>f
| 放大
| 倒立
| 實像
| 與物異側
| v>2f
| 幻燈機
|
u=f
| 無
| 不成像
| 無
| 無
| v=∞
| 特點:虛實分界點
|
u<f
| 放大
| 正立
| 虛像
| 與物同側
| ——
| 放大鏡
|
為了研究各種猜想,人們經常用光具座進行試驗。
蠟燭的燭芯,凸透鏡,光屏應儘量保持在同一高度上。
(3)
凸透鏡成像滿足1/v+1/u=1/f
(1)物體處於2倍焦距以外
(2)物體處於2倍焦距和1倍焦距之間
(3)物體處於焦點以內
對於虛像來說:
(可以和實像一樣記憶,只是虛像的相距為負)
放大倍率:
(虛像也有對應的放大倍率,如果是負值說明是虛像。)
原理套用
鏡頭就是一個凸透鏡,要照的景物就是物體,膠片就是螢幕,照射在物體上的光經過漫反射通過凸透鏡將物體的像成在最後的膠片上,膠片上塗有一層對光敏感的物質,它在曝光後發生
化學變化,物體的像就被記錄在膠捲上。
物體靠近時,像越來越遠,越來越大,最後再同側成虛像。
物遠像近像變小;物近像遠像變大。
凹透鏡
凹透鏡成像規律
對於薄凹透鏡:當物體為實物時,成正立、縮小的
虛像,像和物在透鏡的同側;
 凹透鏡成像規律
凹透鏡成像規律 當物體為虛物,
凹透鏡到虛物的距離為一倍焦距(指絕對值)以內時,成正立、放大的
實像,像與物在透鏡的同側;
當物體為虛物,凹透鏡到虛物的距離為一倍焦距(指絕對值)時,成像於無窮遠;
當物體為虛物,凹透鏡到虛物的距離為一倍焦距以外兩倍焦距以內(均指絕對值)時,成倒立、放大的虛像,像與物在透鏡的異側;
當物體為虛物,凹透鏡到虛物的距離為兩倍
焦距(指絕對值)時,成與物體同樣大小的倒立的虛像,像與物在透鏡的異側;
當物體為虛物,凹透鏡到虛物的距離為兩倍焦距以外(指絕對值)時,成倒立、縮小的
虛像,像與物在透鏡的異側。
如果是厚的彎月形
凹透鏡,情況會更複雜。當厚度足夠大時相當於
伽利略望遠鏡,厚度更大時還會相當於正透鏡。
原理套用
近視眼鏡是凹透鏡,
凹透鏡對光線起發散作用,成一個正立、縮小的虛像,聚焦於視網膜上。
像物同側,v<u
物近像近像變大,物遠像遠像變小
凹凸區別
結構
凸透鏡是由兩面磨成球面的透明鏡體組成
凹透鏡是由兩面都是磨成凹球面透明鏡體組成
對光線作用
凸透鏡主要對光線起會聚作用(面鏡則相反)
凹透鏡主要對光線起發散作用(面鏡則相反)
成像性質
凸透鏡是折射成像,成的像可以是 正、倒;虛、實;放、縮,起聚光作用
凹透鏡是折射成像只能成縮小的正立像,起散光作用
凸面鏡是反射成像
凹面鏡是反射成像
透鏡(包括凸透鏡)是使光線透過,使用光線折後成像的儀器,光線遵守
折射定律;面鏡(包括凸面鏡)不是使光線透過,而是反射回去成像的儀器,光線遵守
反射定律。
凸透鏡可以成倒立放大、等大、縮小的實像或正立放大的虛像。可把平行光會聚於焦點,也可把焦點發出的光線折射成平行光。凹透鏡只能成正立縮小的虛像,主要用擴大視野。
光的折射
在物理上凹鏡和凸鏡都是利用光的折射的原理成像,光學顯微鏡和望遠鏡(包括一部分天文望遠鏡)都是利用
光的折射和光的直線傳播原理製成的,放大鏡和顯微鏡是用於觀測放置在觀測人員近處應予放大的物體的。
(一) 放大鏡的成像原理 表面為曲面的玻璃或其他透明材料製成的光學透鏡可以使物體放大成像,光路圖如圖1所示。位於物方焦點F以內的物AB,其大小為y,它被放大鏡成一大小為y'的虛像A'B'。放大鏡的放大率 Γ=250/f' 式中250--明視距離,單位為mm f'--放大鏡焦距,單位為mm 該放大率是指在250mm的距離內用放大鏡觀察到的物體像的視角同沒有放大鏡觀察到的物體視角的比值。
(二) 顯微鏡的成像原理 顯微鏡和放大鏡起著同樣的作用,就是把近處的微小物體成一放大的像,以供人眼觀察。只是顯微鏡比放大鏡可以具有更高的放大率而已。 圖2是物體被顯微鏡成像的原理圖。圖中為方便計,把物鏡L1和目鏡L2均以單塊透鏡表示。物體AB位於物鏡前方,離開物鏡的距離大於物鏡的焦距,但小於兩倍物鏡焦距。所以,它經物鏡以後,必然形成一個倒立的放大的實像A'B'。 A'B'位於目鏡的物方焦點F2上,或者在很靠近F2的位置上。再經目鏡放大為虛像A''B''後供眼睛觀察。虛像A''B''的位置取決於F2和A'B'之間的距離,可以在無限遠處(當A'B'位於F2上時),也可以在觀察者的明視距離處(當A'B'在圖中焦點F2之右邊時)。目鏡的作用與放大鏡一樣。所不同的只是眼睛通過目鏡所看到的不是物體本身,而是物體被物鏡所成的已經放大了一次的像。
(三) 顯微鏡的重要光學技術參數 在鏡檢時,人們總是希望能清晰而明亮的理想圖象,這就需要顯微鏡的各項光學技術參數達到一定的標準,並且要求在使用時,必須根據鏡檢的目的和實際情況來協調各參數的關係。只有這樣,才能充分發揮顯微鏡應有的性能,得到滿意的鏡檢效果。 顯微鏡的光學技術參數包括:數值孔徑、解析度、放大率、焦深、視場寬度、覆蓋差、工作距離等等。這些參數並不都是越高越好,它們之間是相互聯繫又相互制約的,在使用時,應根據鏡檢的目的和實際情況來協調參數間的關係,但應以保證解析度為準。
1. 數值孔徑
數值孔徑簡寫NA,數值孔徑是物鏡和聚光鏡的主要技術參數,是判斷兩者(尤其對物鏡而言)性能高低的重要標誌。其數值的大小,分別標刻在物鏡和聚光鏡的外殼上。 數值孔徑(NA)是物鏡前透鏡與被檢物體之間介質的折射率(n)和孔徑角(u)半數的正弦之乘積。用公式表示如下:NA=nsinu/2 孔徑角又稱"鏡口角",是物鏡光軸上的物體點與物鏡前透鏡的有效直徑所形成的角度。孔徑角越大,進入物鏡的光通亮就越大,它與物鏡的有效直徑成正比,與焦點的距離成反比。 顯微鏡觀察時,若想增大NA值,孔徑角是無法增大的,唯一的辦法是增大介質的折射率n值。基於這一原理,就產生了水浸物鏡和油浸物鏡,因介質的折射率n值大於1,NA值就能大於1。 數值孔徑最大值為1.4,這個數值在理論上和技術上都達到了極限。2013年,有用折射率高的溴萘作介質,溴萘的折射率為1.66,所以NA值可大於1.4。 這裡必須指出,為了充分發揮物鏡數值孔徑的作用,在觀察時,聚光鏡的NA值應等於或略大於物鏡的NA值。 數值孔徑與其他技術參數有著密切的關係,它幾乎決定和影響著其他各項技術參數。它與解析度成正比,與放大率成正比,與焦深成反比,NA值增大,視場寬度與工作距離都會相應地變小。
2. 解析度
顯微鏡的解析度是指能被顯微鏡清晰區分的兩個物點的最小間距,又稱"鑑別率"。其計算公式是σ=λ/NA 式中σ為最小分辨距離;λ為光線的波長;NA為物鏡的數值孔徑。可見物鏡的解析度是由物鏡的NA值與照明光源的波長兩個因素決定。NA值越大,照明光線波長越短,則σ值越小,解析度就越高。要提高解析度,即減小σ值,可採取以下措施(1) 降低波長λ值,使用短波長光源。(2) 增大介質n值以提高NA值(NA=nsinu/2)。(3) 增大孔徑角u值以提高NA值。(4) 增加明暗反差。
3.放大率和有效放大率
由於經過物鏡和目鏡的兩次放大,所以顯微鏡總的放大率Γ應該是物鏡放大率β和目鏡放大率Γ1的乘積: Γ=βΓ1 顯然,和放大鏡相比,顯微鏡可以具有高得多的放大率,並且通過調換不同放大率的物鏡和目鏡,能夠方便地改變顯微鏡的放大率。 放大率也是顯微鏡的重要參數,但也不能盲目相信放大率越高越好。顯微鏡放大倍率的極限即有效放大倍率。 解析度和放大倍率是兩個不同的但又互有聯繫的概念。有關係式:500NA<Γ<1000NA 當選用的物鏡數值孔徑不夠大,即解析度不夠高時,顯微鏡不能分清物體的微細結構,此時即使過度地增大放大倍率,得到的也只能是一個輪廓雖大但細節不清的圖像,稱為無效放大倍率。反之如果解析度已滿足要求而放大倍率不足,則顯微鏡雖已具備分辨的能力,但因圖像太小而仍然不能被人眼清晰視見。所以為了充分發揮顯微鏡的分辨能力,應使數值孔徑與顯微鏡總放大倍率合理匹配。
4. 焦深
焦深為焦點深度的簡稱,即在使用顯微鏡時,當焦點對準某一物體時,不僅位於該點平面上的各點都可以看清楚,而且在此平面的上下一定厚度內,也能看得清楚,這個清楚部分的厚度就是焦深。焦深大, 可以看到被檢物體的全層,而焦深小,則只能看到被檢物體的一薄層,焦深與其他技術參數有以下關係:(1) 焦深與總放大倍數及物鏡的數值孔徑成反比。(2) 焦深大,解析度降低。 由於低倍物鏡的景深較大,所以在低倍物鏡照相時造成困難。在顯微照相時將詳細介紹。 5. 視場直徑(Field Of View) 觀察顯微鏡時,所看到的明亮的圓形範圍叫視場,它的大小是由目鏡里的視場光闌決定的。視場直徑也稱視場寬度,是指在顯微鏡下看到的圓形視場內所能容納被檢物體的實際範圍。視場直徑愈大,愈便於觀察。有公式 F=FN/β 式中F: 視場直徑,FN:視場數(Field Number, 簡寫為FN,標刻在目鏡的鏡筒外側),β:物鏡放大率。由公式可看出:(1) 視場直徑與視場數成正比。(2) 增大物鏡的倍數,則視場直徑減小。因此,若在低倍鏡下可以看到被檢物體的全貌,而換成高倍物鏡,就只能看到被檢物體的很小一部份。 6. 覆蓋差 顯微鏡的
光學系統也包括蓋玻片在內。由於蓋玻片的厚度不標準,光線從蓋玻片進入空氣產生折射後的光路發生了改變,從而產生了相差,這就是覆蓋差。覆蓋差的產生影響了顯微鏡的成響質量。 國際上規定,蓋玻片的標準厚度為0.17mm,許可範圍在0.16-0.18mm,在物鏡的製造上已將此厚度範圍的相差計算在內。物鏡外殼上標的0.17,即表明該物鏡所要求的蓋玻片的厚度。 7. 工作距離WD 工作距離也叫物距,即指物鏡前透鏡的表面到被檢物體之間的距離。
三招巧記成像規律
在透鏡知識的學習中,凸透鏡成像規律及其套用是一個重點內容,儘管我們都是通過實驗來研究凸透鏡的成像情況的,但在實際練習時仍然會把規律遺忘導致做題時感到困難。現介紹幾招記憶技巧,供大家參考:
第一招:列表記憶法(f為凸透鏡的焦距)
由凸透鏡成像的規律表可以看出:
1. 凸透鏡成實像的特點是物體在焦點以外。當物體從2倍
焦距以外向焦點移動的過程中,
物距逐漸減小,
像距逐漸增大,像也逐漸變大,像和物體一定在
凸透鏡的異側,並且像是倒立的。
2. 凸透鏡成
虛像的特點是凸透鏡成虛像時,像和物體一定是在透鏡的同側,並且像是正立、放大的。
3. 從表中看出,有三個“沒有”:沒有正立的
實像;沒有倒立的虛像;沒有縮小的虛像。
說明:
1. 焦點F是凸透鏡成實像和虛像的分界點。
當物體放在凸透鏡的焦點上(即物距u等於焦距f)時,既不成實像也不成虛像,因為從焦點發出的光線經過凸透鏡折射後與主光軸平行射出,平行光不能相交,所以不能成像。
當物體放在焦點以外時成實像,當物體放在焦點以內時成虛像,即物體成像以焦點F分為界點,分成虛像和成實像的區域,物體的位置分別在成虛像和實像的區域時,所成的像就對應數軸圖上的規律。
2. 2倍焦距處是凸透鏡成放大實像和縮小實像的分界點,物體在2倍焦距處成等大的實像,在2倍焦距以外成縮小的實像,在1倍和2倍焦距之間成放大的實像。
第三招:口訣記憶法
1倍焦距分虛實,2倍焦距分大小;
實像與物異側倒,物遠像近像變小;
虛像與物同側正,巧記口訣活用好。
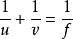
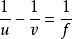
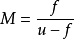
 凹透鏡成像規律
凹透鏡成像規律


