N色定理

N色定理是指在一個物體上不同區域染色，需要多少種顏色的問題。

基本介紹

• 中文名：N色定理
• 時間：1852；1974。
• 國家：英國
• 提出：古德里安和林格

一，來源

1974年，德國數學家林格和美國數學家楊斯證明了，在曲面上作圖，有以下定理：

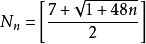
,(參見《圖論導引》214頁，機械工業出版社；人民郵電出版社258頁)

其中方括弧[ ]表示整數部分，n表示洞的個數。

二，n的不同值

（一）在平面中4個或者4個以下的區域

可以構成兩兩相連的區域，可以一筆劃。

圖1。每個區域必須是單連通的，就是一個區域不能夠是分成2塊或者2塊以上。這是著名的四色猜想。大家知道，平面上不可能有兩兩相通的5個區域。注意，兩兩相連是未來網路樞紐的要求。

平面上4個區域兩兩相連圖1

在一個輪胎形狀的環面的表面

7個或者7個以下的區域可以構成兩兩相連的區域。可以“一筆劃”。

圖1—1（右則）上下對摺以後，再左右對摺，形成一個輪胎狀，7個區域兩兩相連（國外數學家給出）.兩兩相連的區域可以不經過其它區域到達任何一個區域。P。J希伍德以畢生精力研究四色定理，並且證明了5色定理，稀伍德考察了一般曲面著色問題提出一個推測：在有P>1個洞的封閉曲面上，足以為任何地圖著色的最小數等於

。其中[X]表示整數部分，即圖（2)

圖2-1

圖2-2背面

.

圖2-3正面

（二）在有2個洞的雙環面

有8個區域兩兩相連（圖2）

例如兩個洞的曲面應該 。（見圖3右下圖）王曉明經過9年完成。

注意，研究兩兩相連區域是因為網路戰爭的需要。在一個兩兩相連的樞紐，交通是不會堵塞的。

下面的兩個圖是一回事，上下對摺，再左右對摺，就是一個輪胎形狀，有6個區域兩兩相連，再把有區域7和區域8的管子安裝到相應部位，就是一個有兩個洞的曲面，有8個區域兩兩相連（上面是圖片，下面是依據圖片製作的模型，王曉明構造，製作模型，充分說明林格和楊斯的證明是正確的）。

圖3-1八色定理圖片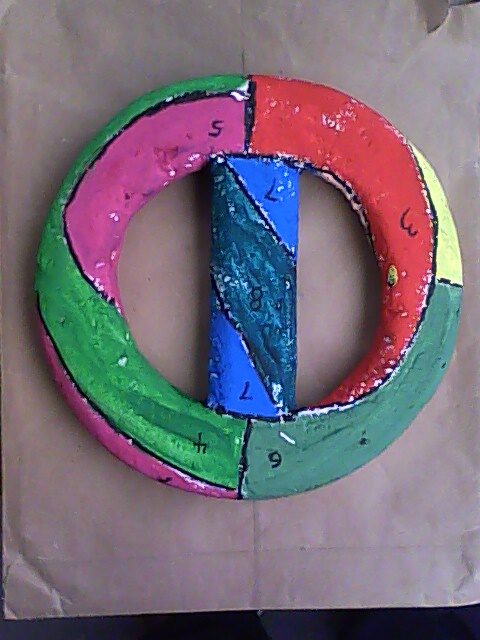

正面

依據圖片製作的模型正面

　　

　　

　　

　　

　　

　　

　　

　　

　　

　　

（三），在有三個洞的曲面上

有9個區域兩兩相連（圖4）

是在圖2的基礎上（7個區域兩兩相連）加上一個三叉，下圖三叉對應上圖的相應位置，就是一個方向盤形狀的虧格3的9個兩兩相連區域參見圖5， .

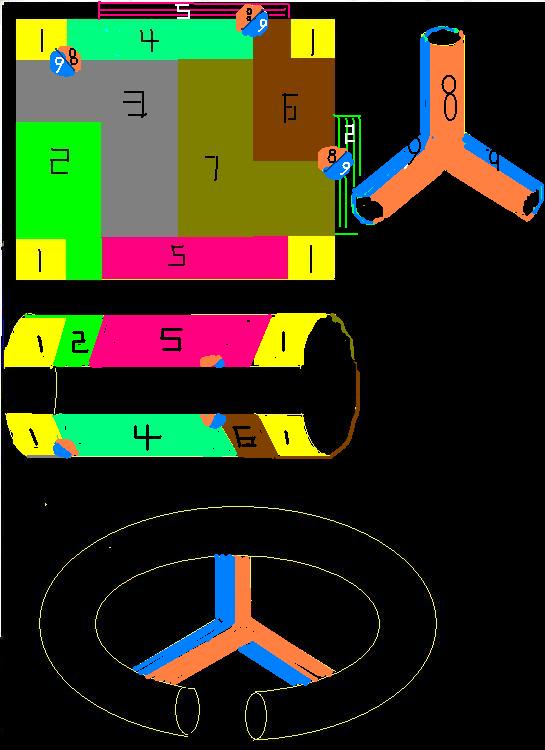圖4-1虧格3時有9個區域兩兩相連

王曉明構造（上面是圖片，下面兩個是依據圖片製作的模型）。

圖4-3，背面

圖4-2，九色圖片模型

（四），虧格為4時

有10個兩兩相連區域（圖4）

參見圖5：

在圖2的基礎上，上圖上下對摺，再左右對摺成為一個輪胎形狀，下圖四叉按照ABCD位置對應上圖，就是一個有4個洞的10個兩兩相連區域參見圖6,因為林格證明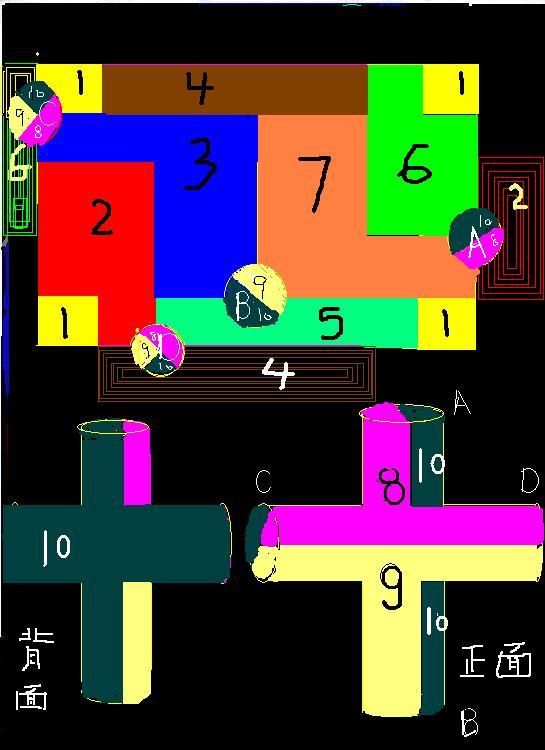

圖5--4個洞的10個兩兩相連區域圖5

，王曉明完成（右邊是依據圖片製作模型，有10個區域兩兩相連）。

十色定理圖片模型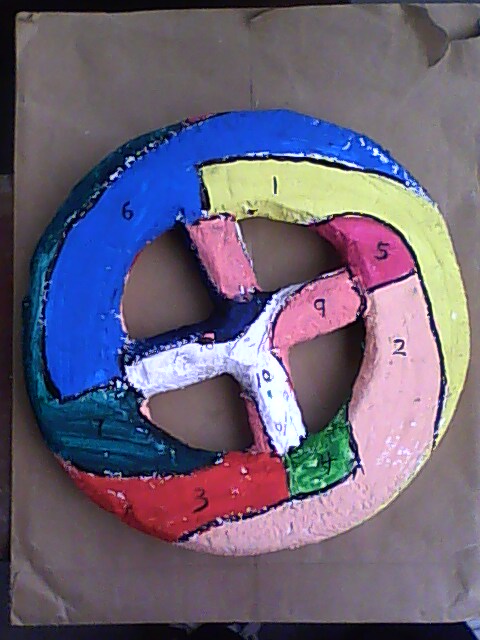

背面

　　

（五），虧格5時11個區域兩兩相連

（圖6）

參見圖6，下面圖上下對摺再左右對摺形成一個輪胎，有7個區域兩兩相連，把上面的五叉按照ABCD對應安裝上去，就是一個有11個區域兩兩相連。林格1974年證明， 。王曉明構造，湖南李恆嘉安裝。

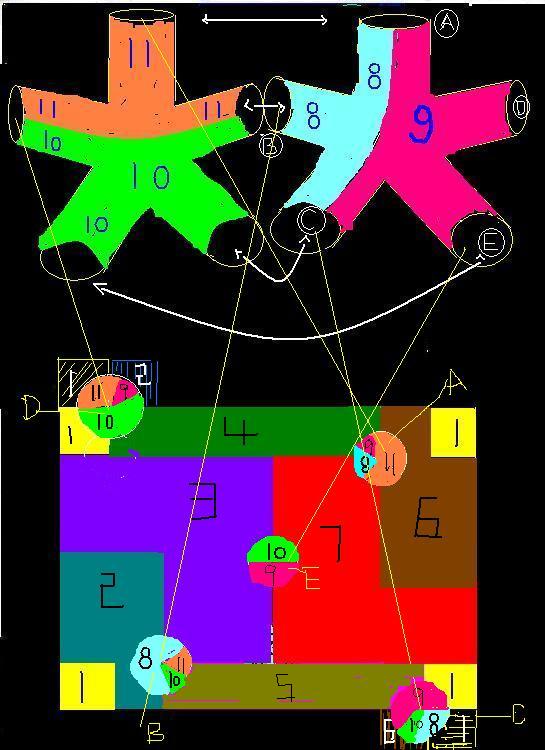圖6，有5個洞的曲面有11個區域兩兩相連

（六），虧格7時有12個區域兩兩相連

，參見圖7，右上圖是外環平面圖，有6個區域兩兩相連，先上下對摺，再左右對摺，左右對摺時一段輕輕扭轉，使得1對著5,2對著6,3對著4。右下圖和左下圖是內環，上下對摺再左右對摺形成一個輪胎形狀，左右對摺時一端輕輕扭轉，使得7對摺11,8對著12,9對摺10。外部有6根柱子與外環相連，形成一個有7個洞的12個區域兩兩相連，王曉明構造。

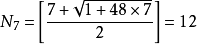
圖7，有12色個區域兩兩相連，定理。

三，可以構造任意多個兩兩相連區域

1，前言

大自然的運行有兩種模式，一種是由一到多，例如樹木由一根主幹生長到很多樹枝樹葉，人類祖先最開始只有亞當和夏娃再到數千人到現在70億；另一種是由多到一，例如千萬的山間小溪匯集江河最後到海，再一個就是人類的知識，由多學科多門類融合到一個總理論。

科學最讓人不可思議的是它的融合，無數自然現象可以歸結為物理學、化學、生物學、....。

今天的文章注定是一個載入史冊，它是人類思維的輝煌壯舉，它把數學中最經典的哥德巴赫猜想、費馬大定理、黎曼猜想、歐拉公式和廣義相對論量子理論的m理論融合在一個模型里。

作者王曉明在瑞典-斯德哥爾摩市政廳

,

2，從四色定理開始

法蘭西斯·古德里於1831年生於倫敦，在1852年提出的猜想，只需要四種顏色為地圖著色。這是因為他發現在平面上或者球面上，只能有4個區域兩兩相連，英國數學家德摩根證明了平面上不存在5個區域兩兩相連。

1974年德國的林格和美國的楊斯證明了在曲面上染色定理，例如，在一個汽車輪胎形狀的環面需要7種顏色，因為可以構造7個兩兩相連的區域，6種顏色肯定不夠的；在有兩個洞的雙環面需要8種顏色，因為可以構造8個兩兩相連的區域，7種顏色肯定不夠的；....。

3，可以構造無窮多個兩兩相連區域

如果一般人不能理解，我慢慢道來：現在有兩根管子，一個記為1，一個記為2，它們代表兩個區域。我們假定所有的管子都是可以隨意拉伸和彎曲的。把兩根管子端端相連，就是一個汽車輪胎一樣的環，它有兩個區域，我們再用一根直管子記為3，安在這個環的中間，一頭連著區域1，一頭連著區域2，現在它是有兩個洞的雙環了，有三個區域兩兩相連。
現在我們用一個“丁”字型的三叉管，記為區域4，三個連線埠分別與區域1，區域2，區域3相連。於是現在有4個區域兩兩相連；
我們再用一根四叉管記為區域5,4個連線埠分別與區域1,2,3,4相連，現在有5個區域兩兩相連。
這個步驟可以無限制進行下去，用五叉管，六叉管，。.。構造無窮多個區域，它們都是兩兩相連的。

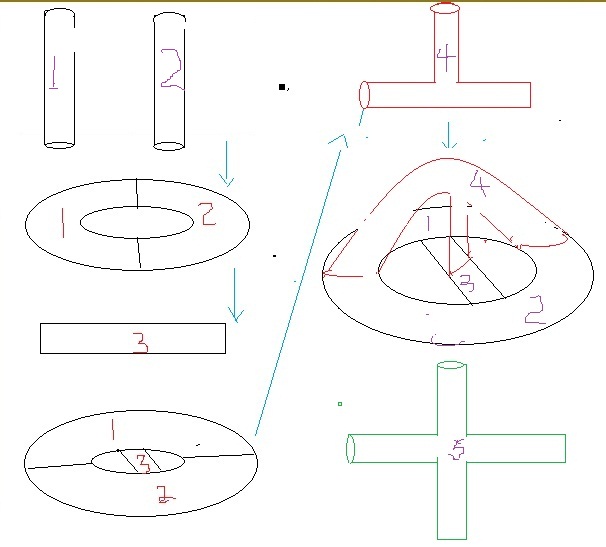圖8，無窮多個兩兩相連區域的具體構造方法

4，圖論與數論聯繫起來

數學家和物理學家把上面（圖8中的）這個叫做岐管。
區域1，代表第一個素數2;；第二個區域代表第二個素數3；....；第n個區域代表第n個素數。

在數論中，最重要的元素就是素數，歐幾里得證明了有無窮多個素數，並且它們有一個特點就是兩兩互素。無窮多個兩兩互素的素數與無窮多個兩兩相連區域一一對應。

圖論與數論聯繫起來了。

我們把這個圖8中的岐管倒過來，就像一個網子，籃球網子。籃球網子是把籃球往裡面投。

岐管或者稱為篩子

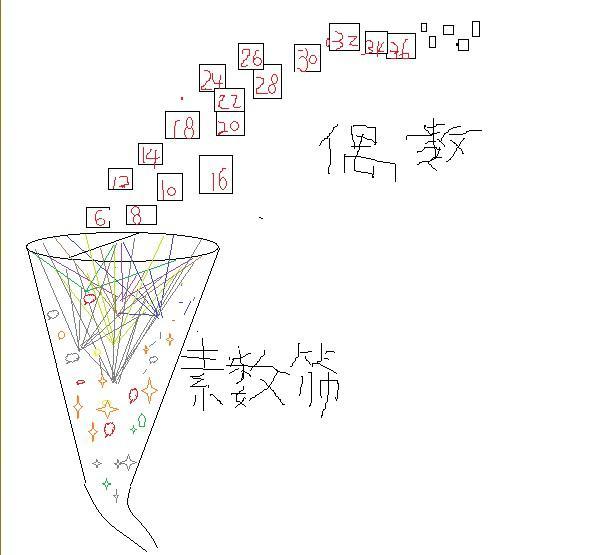圖9，岐管，篩子

5，篩子

公元前300年古希臘有一個數學家叫做埃拉特斯特尼，他把這個網子當成篩子，把自然數往裡面扔，他說凡是合數通過篩子以後就會從網子裡面篩掉，留下的是素數，這個就是著名的埃拉特斯特尼篩法。

圖9，我們上面這個岐管篩子是把偶數往裡面扔，哥德巴赫說，大於4的偶數一個也不會漏出篩子，除了6=3+3以外，其他偶數都是可以在不同的素數區域被攔截。例如8會在區域2也就是素數3和素數5（第三個區域）被攔截；偶數10會在素數3和素數7的兩個區域之間被攔截；。.。總之，無窮多個偶數都逃不脫這個網子，沒有一個偶數可以漏到外面去。（右圖）
看到沒有？數論與圖論已經融合一起了。

6，與費馬大定理聯繫起來

這個還不算神奇，這個岐管的內部空間我們記為X，外部空間記為Y，它有很多洞,可以有無窮多個洞，可以有無窮多個空間維度n，宇宙內外整體記為1，就是說Xⁿ+Yⁿ=1，這個叫做費馬曲線，它是由費馬大定理Aⁿ+Bⁿ=Cⁿ同時除以Cⁿ得到的。
費馬大定理與哥德巴赫猜想聯繫起來了。

7，費馬大定理的岐管就是m理論岐管

物理學家認為，宇宙是10維空間或者11維空間，或者26維空間等5個版本。還有物理學家認為有無窮多個維度的空間。他們管這個理論叫做玄理論或者M理論，是把廣義相對論與量子理論結合一起的終極理論，霍金說是最後的理論。

在弦/m理論的11維空間裡，有4維空間的伸展，7維空間捲縮起來的。 幾何體的拓撲性質同粒子緊密相關。例如，這種粒子幾何體有幾個洞，決定著粒子世代的數目，在這些捲縮維度的空間裡所採取的幾何構型決定著弦或者膜能夠有什麼樣的震動模式，從而決定著各種粒子的質量、自旋、以及電荷等各種相互作用的耦合常數。

原來，不僅僅自旋和同位旋等內部變數和內部空間都出自這些多維空間的幾何學，而且粒子的電荷質量等性質，無一不是從這裡產生出來的，不僅僅如此，甚至我們生活本身也通過三維空間和一維時間都是從類似的幾何體的構造中生長出來的。 我們生活在高維宇宙的一小片中，大到銀河宇宙，小至原子夸克，都是 弦線構成的。

8，計算岐管中的線段需要黎曼猜想

數學家考慮的是怎樣計算這個岐管上的區域或者計算區域上面的一個點。如果岐管上某一個區域n，在n上的一個點是1/n，因為這個岐管有無窮多個維度，或者很多維度，我們要定位這個點，就要考慮它的管壁——實部，還有考慮它的內外空間位置——虛部，即，s=α+βi，i 表示虛數，看出名堂來沒有？

黎曼猜想！

在弦/m理論中，管壁就是膜，如果把膜上面的一個點定位，假設這個點是在區域的管壁上，膜是一個沒有厚度的管壁，管壁上的點就是實部，管壁內外就是虛部。

管壁上實部為1/2，因為宇宙等於1（xⁿ+yⁿ=1）這個管壁就是實部α，確定這個點的位置還有考慮管壁內外空間結構，就是虛部，要計算這個零點，就要用黎曼函式來運算，黎曼猜想！

黎曼猜想與費馬大定理聯繫起來了。

9，與歐拉公式聯繫起來

虛部怎麼計算呢？岐管內部看成一個圓管，虛部是什麼？它至少應該有管道內或者管道外中的一個參數。假設管道截面是一個圓，管道

內的截面圓依然是二維平面，在岐管上的一個點，就是一個圓。大家知道歐拉公式嗎？

。

以 開始，以相對速度π，走了 時間（虛時間），再加1，回到原點。

虛時間是為了對應時間起點（大爆炸）而定義的一個概念。在虛時間這個概念體系里，在比三維更高的維度空間，時間並不是一條直線，而是一個閉合的圓，沒有起始也沒有終結，宇宙的起點如果源自大爆炸，那在此之前的時間將無法定義。因此，為了解決奇點之前時間應該如何，我們引用到了複數的概念。

10,與愛因斯坦方程的聯繫

質能方程E=mc²，E表示能量，m代表質量，而c則表示光速。在上面的岐管表面是C，它的平方就是光速掃過的面積。這個費馬方程岐管，弦/m理論高維空間認為這個麵團裡面是空心的，就是說，這個麵團戳了一些貫通的洞以後，再把麵團內部看成一個空心的，這個曲面只是一個沒有厚度的膜。

可以擴展到許許多多的內容