基本介紹
- 中文名:Quine-McCluskey算法
- 外文名:
- 概述:奎因-麥克拉斯基算法
- 簡介:Quine-McCluskey 算法是最小
- 方法:找到這個函式的所有素蘊涵
算法簡介,方法,複雜性,實例,
算法簡介
它在功能上等同於卡諾圖,但是它的表格形式使它更有效的用做計算機算法,並且它還給出了檢查布爾函式是否達到了最小化形式的確定性方法。
方法
涉及兩步:
找到這個函式的所有素蘊涵項(也叫質蘊涵項)。
使用這些素蘊涵項(implicant)來找到這個函式的本質素蘊涵項(也叫實質蘊涵項),對覆蓋這個函式是必須的其他素蘊涵項也同樣要使用。
複雜性
儘管在處理多於四個變數的時候比卡諾圖更加實用,Quine-McCluskey 算法也有使用限制,因為它解決的問題是NP-完全的: Quine-McCluskey 算法的運行時間隨輸入大小而呈指數增長。可以證明對於 n 個變數的函式,素蘊涵項的數目的上界是 3n/n。如果 n = 32,則可能超過 6.1 * 1014,或 617 萬億個素蘊涵項。有大量變數的函式必須使用潛在的非最優的啟發式方法來最小化。
實例
最小化一個任意的函式:
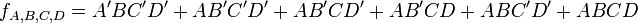
m0 | 0 | 0 | 0 | 0 | 0 | |
m1 | 0 | 0 | 0 | 1 | 0 | |
m2 | 0 | 0 | 1 | 0 | 0 | |
m3 | 0 | 0 | 1 | 1 | 0 | |
m4 | 0 | 1 | 0 | 0 | 1 | |
m5 | 0 | 1 | 0 | 1 | 0 | |
m6 | 0 | 1 | 1 | 0 | 0 | |
m7 | 0 | 1 | 1 | 1 | 0 | |
m8 | 1 | 0 | 0 | 0 | 1 | |
m9 | 1 | 0 | 0 | 1 | x | |
m10 | 1 | 0 | 1 | 0 | 1 | |
m11 | 1 | 0 | 1 | 1 | 1 | |
m12 | 1 | 1 | 0 | 0 | 1 | |
m13 | 1 | 1 | 0 | 1 | 0 | |
m14 | 1 | 1 | 1 | 0 | x | |
m15 | 1 | 1 | 1 | 1 | 1 |
你能輕易的形成這個表的規範的積之和表達式,簡單的通過總和這個函式求值為一的那些極小項:
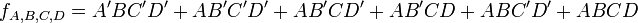
第一步找到素蘊涵項
當然,這的確不是最小化的。為了最佳化,所有求值為一的極小項都首先放到極小項表中,不關心項也可以加入這個表中與極小項組合:
1 | m4 | 0100 |
m8 | 1000 | |
2 | m9 | 1001 |
m10 | 1010 | |
m12 | 1100 | |
3 | m11 | 1011 |
m14 | 1110 | |
4 | m15 | 1111 |
現在你可以開始把極小項同其他極小項組合在一起。如果兩個項不同只是一個單一的數字,則可以這個數字替代為一個橫槓,來指示這個數字無關緊要。不再組合的項標記上 "*"。
1 | m4 | 0100 | m(4,12) -100* | m(8,9,10,11) 10--* |
m8 | 1000 | m(8,9) 100- | m(8,10,12,14) 1--0* | |
-- | -- | -- | m(8,10) 10-0 | -- |
2 | m9 | 1001 | m(8,12) 1-00 | m(10,11,14,15) 1-1-* |
m10 | 1010 | -- | -- | |
m12 | 1100 | m(9,11) 10-1 | -- | |
-- | -- | -- | m(10,11) 101- | -- |
3 | m11 | 1011 | m(10,14) 1-10 | -- |
m14 | 1110 | m(12,14) 11-0 | -- | |
4 | m15 | 1111 | m(11,15) 1-11 | -- |
m(14,15) 111- |
第二步找到本質素蘊涵項
沒有項可以繼續進一步這樣組合,所以現在我們構造一個本質素蘊涵項表。縱向是剛才生成的素蘊涵項,橫向是早先指定的極小項。
4 | 8 | 10 | 11 | 12 | 15 | => | A | B | C | D | ||
m(4,12)* | X | X | -100 | => | - | 1 | 0 | 0 | ||||
m(8,9,10,11) | X | X | X | 10-- | => | 1 | 0 | - | - | |||
m(8,10,12,14) | X | X | X | 1--0 | => | 1 | - | - | 0 | |||
m(10,11,14,15)* | X | X | X | 1-1- | => | 1 | - | 1 | - |
這裡的每個本質素蘊涵項都標記了星號 - 第二個素蘊涵項能被第三個和第四個所覆蓋,而第三個素蘊涵能被第二個和第一個所覆蓋,因此都不是本質的。如果一個素蘊涵項是本質的,則同希望的一樣,它必須包含在最小化的布爾等式中。在某些情況下,本質素蘊涵形不能覆蓋所有的極小項,此時可採用額外的簡約過程。最簡單的“額外過程”是反覆試驗,而更系統的方式是Petrick方法。在當前這個例子中,本質素蘊涵項不能處理所有的極小項,你可以組合這兩個本質素蘊涵項於兩個非素蘊涵項中的一個而生成: