基本介紹
- 中文名:H碼
- 外文名:Huffman Coding
- 發表人:David.A.Huffman
- 時間:1952年
- 別名:哈夫曼編碼或霍夫曼編碼
- 類型:程式算法
關於霍夫曼編碼,特點,步驟,
關於霍夫曼編碼
霍夫曼編碼方案是由David A Huffman在1952年開發的。這個算法依據數據的出現頻率來編碼數據從而可達到數據壓縮的目的。用於編碼數據的數據結構是一棵加權的二進制樹,又叫霍夫曼樹。
霍夫曼樹有幾個特性:
1.霍夫曼樹必須是一棵二進制樹;
2.霍夫曼樹是加權的,在數據流中出現頻繁的元素在樹的頂部,而很少出現的元素沉到樹的底部;
3.霍夫曼樹的每一個左邊的分支分配一個0(或1)值,而每一個右邊的分支賦值為1(或O)。
為了構造一棵霍夫曼樹,需對數據進行兩步操作。首先,構造一個唯一數據元素集和它們的頻率的列表。這個列表按頻率的升值排列。就是說,出現頻率最高的數據元素排在表的下部。然後,構造實際的霍夫曼樹。選擇頻率最低的兩個元素組成樹的葉。兩片葉的父節點是它們的頻率之和。這棵樹被插入到列表中(由父節點的值來決定插到列表中的位置),而剛才用於組成這棵樹的兩個葉子被從列表中移除。繼續這個過程直到列表中只留下一個元素,它就是最終的霍夫曼樹的父節點。
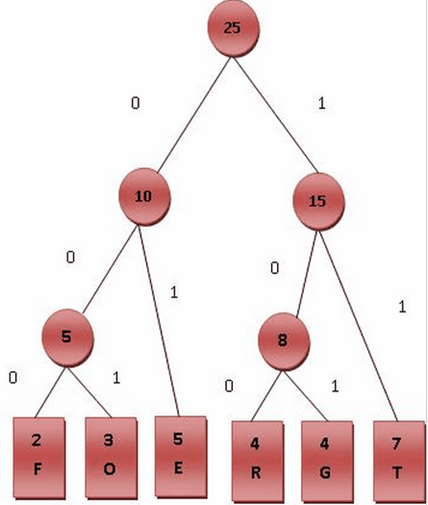
為了將霍夫曼樹用於編碼數據,必須建立一種能唯一確定樹中的每一個值的方法。具體做法是把樹的每一個左邊分支賦值為0,而把每一個右邊分支賦值為1。從樹的根開始,找到每一個葉.把沿途經過的左、右分支的值按順序排列,就可以用1和0的序列來唯一地標識樹中的每一個元素了。
對於數據壓縮最後要做的是,遍歷原始數據的每一個元素,把與每一個數據元素相關的霍夫曼代碼寫到輸出檔案。因為起碼大多數數據元素的霍夫曼表示比它們本來的表示位數要少,於是達到壓縮的目的。為了此後解碼的需要,原來的編碼信息(霍夫曼樹和所生成的數據表)也必須存儲在輸出檔案中。
哈夫曼編碼是依據符號出現的機率對符號進行編碼,需要對原始數據掃描兩遍。第一遍掃描要精確統計原始圖像中每個灰度值出現的機率,第二遍是建立哈夫曼二叉樹並進行編碼,故數據壓縮和還原速度較慢,但此法有效簡單,且編碼效率高,所以在一些圖像壓縮標準中被普遍採用。
特點
主要特點如下。
(1)Huffman編碼的構造順序明確,但碼不是唯一的。因為在為兩個分支賦值時,可以是左支(或上支)為0,也可以是右支(或下支)為0,造成編碼的不惟一。此外,當兩個符號的機率相等時,誰前誰後也是隨機的,構造出來的碼字就不是惟一的。
(2)Huffman編碼的字長參差不齊,硬體實現不是很方便。
(3)Huffman編碼在機率分布很不均勻時能夠具有顯著的效果,而在信源分布均勻時,一般不使用Huffman編碼。
(4)對信源進行Huffman編碼後,形成了一個Huffman編碼表。解碼時,必須參照Huffman編碼表才能正確解碼。
理論研究表明,Huffman編碼是一種接近壓縮比上限的編碼方法,因此它被廣泛用於多種壓縮算法之中。
步驟
Huffman編碼的基本步驟如下。
(1)進行數據統計,統計不同信息符號出現的機率。
(2)將信號源的符號按照出現機率遞減的順序排列。
(3)將最下面的兩個最小出現機率進行合併相加,得到的結果作為新符號的出現機率。
(4)重複進行步驟1和2直到機率相加的結果等於1為止。
(5)在合併運算時,機率大的符號用編碼0表示,機率小的符號用編碼1表示。
(6)記錄機率為1處到當前信號源符號之間的0,l序列,從而得到每個符號的編碼。