機器博弈是人工智慧研究的重要分支,人類對機器博弈的研究衍生了大量的研究成果。Alpha -Beta 搜尋算法是機器博弈領域中最為重要的算法之一。
基本介紹
- 中文名:Alpha-Beta搜尋算法
- 外文名:Alpha-Beta搜尋算法
- 別稱:Alpha-Beta剪枝
- 套用學科:計算機
- 適用領域範圍:計算機博弈
概念,實現,效率分析,示例代碼,
概念
在極大極小搜尋的過程中,存在著2 種明顯的冗餘現象:
第1 種現象是極大值冗餘。在圖1中,節點A 的值應是節點 B 和節點C 的值中之較大者。現在已知節點 B 的值大於節點D 的值。由於節點C 的值應是它的諸子節點的值中之極小者,此極小值一定小於等於節點D 的值,因此亦一定小於節點B 的值,這表明,繼續搜尋節點C 的其他諸子節點E ,F ...已沒有意義,它們不能做任何貢獻,於是把以節點 C 為根的子樹全部剪去。這種最佳化稱為Alpha 剪枝。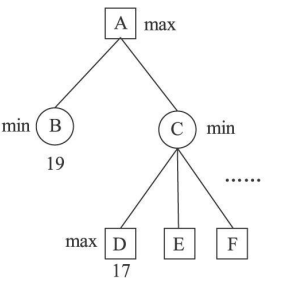 極大值冗餘
極大值冗餘
 極大值冗餘
極大值冗餘在圖b是與極大值冗餘對偶的現象,稱為極小值冗餘。節點A 的值應是節點B 和節點C 的值中之較小者。 現在已知節點B 的值小於節點D 的值。 由於節點C 的值應是它的諸子節點的值中之極大者,此極大值一定大於等於節點 D 的值,因此也大於節點B的值,這表明,繼續搜尋節點C 的其他諸子節點已
沒有意義,並可以把以節點C 為根的子樹全部剪去,這種最佳化稱為Beta剪枝。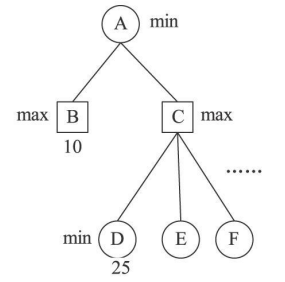 極小值冗餘
極小值冗餘
沒有意義,並可以把以節點C 為根的子樹全部剪去,這種最佳化稱為Beta剪枝。
 極小值冗餘
極小值冗餘把Alpha -Beta 剪枝套用到極大極小算法中,就形成了Alpha -Beta搜尋算法。
實現
在搜尋過程中,max 方節點的當前最優值被稱為α值,min 方節點的當前最優值被稱為β 值。在搜尋開始
時,α 值為-∞,β值為+∞,在搜尋過程中,max 節點使α 值遞增,min 節點則使 β值遞減,兩者構成一個區
間[ α ,β] ,這個區間被稱為視窗。視窗的大小表示當前節點值得搜尋的子節點的價值取值範圍,向下搜尋
的過程就是縮小視窗的過程,最終的最優值將落在這個視窗中。一旦max 節點得到其子節點的返回值大於
β值或min 節點得到其子節點的返回值小於α 值,則發生剪枝。具體算法如下所示:
1)A lpha -Be ta算法,入口參數為( P ,α , β, d),其中P 是節點,[ α ,β]是初始視窗,d 是搜尋深度;
2)若P 為葉節點,則取靜態估計值返回;
3)產生P 的所有合理著法mi ,1≤i≤n ;
4)v=-∞;
5)i=1;
6)由著法 mi 生成子節點P i ;
7)t=-A lpha -Be ta( Pi , -β, -α , d -1) ( 遞歸調用下一層);
8)若t>v ,則v =t ,否則,轉11);
9)若v>α ,則 α =v;
10)若v≥β,則取v 值返回;
11)i=i+1;
12)若i≤n ,則轉6);
13)取v 值返回;
該算法使用了負極大值原理,算法只檢查是否出現β剪枝,而不需檢查是否有 α 剪枝。在Alpha -Beta 搜尋中,有 3 種不同類型的評價值:高出邊界型( fail high),由於發生了剪枝,只知道返回評分至少是 β ,不知道具體值;低出邊界型( faillow),由於沒找到較好著法,只知道返回評分最多是α ,不知道具體值; 精確型,即返回評分在α 和β之間。
效率分析
將搜尋樹平均分枝因子數記作b ,搜尋深度記作 d ,那么採用極大極小算法搜尋的節點數為

1975 年,Knuth 等證明了,在節點排列最理想的情形下,使用A lpha -Be ta剪枝生成的節點數目為
d為偶數:


d為奇數:

這個數字大約是極大極小算法搜尋節點數的平方根的2 倍左右。那么根據公式

我們得出:如果著法順序的排列最為理想,那么在同樣的情況下,我們可以搜尋原來深度( 即不用A lpha -Beta 剪枝時的深度) 的2 倍。
由於A lpha -Beta 剪枝與節點的排列順序高度相關尋找有效手段將候選著法排列調整為剪枝效率更高的順序就顯得尤為重要了。
示例代碼
C代碼示例
int AlphaBeta(int depth, int alpha, int beta) { if (depth == 0) //如果是葉子節點(到達搜尋深度要求) return Evaluate(); //則由局面評估函式返回估值 GenerateLegalMoves(); //產生所有合法著法 while (MovesLeft()) //遍歷所有著法 { MakeNextMove(); //執行著法 int val = -AlphaBeta(depth - 1, -beta, -alpha); //遞歸調用 UnmakeMove(); //撤銷著法 if (val >= beta) //裁剪 { if (val > alpha) //保留最大值 alpha = val; return beta; } } return alpha; } 