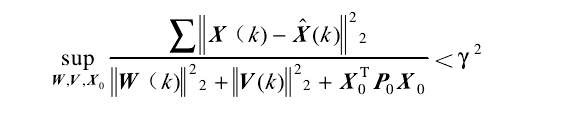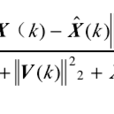魯棒濾波器

濾波是以測量信號為基礎對系統內部不可測量的信號進行估計，系統模型存在不確定情況下的濾波問題即魯棒濾波問題。

在很多的工業套用中，系統中含有不確定參數，精確的系統模型是很難獲得的。為了克服這個困難，引入了魯棒濾波方法。

魯棒濾波器是指考慮系統中的不確定性，設計濾波器使得濾波誤差系統漸近穩定，並且滿足所提出的性能指標。

基本介紹

• 中文名：魯棒濾波器
• 外文名：Robust filter
• 類別：控制科學與工程
• 套用：航天、航海、工業過程等
• 優點：無需了解噪聲的特性等
• 研究方法：魯棒H∞濾波等

研究現狀

魯棒濾波

lyapunov穩定性理論是在時間域中研究參數不確定系統的魯棒分析和綜合問題的主要理論基礎。在這一框架內主要有兩種研究方法，即Riccati方程處理方法和線性矩陣不等式方法。

Riccati方法是早期的一種主要研究方法。它是通過將不確定系統的分析和綜合問題轉化為一個Riccati型矩陣方程(或矩陣不等式)的可解性問題，進而通過求解Riccati方程來對系統的魯棒穩定性及魯棒性能進行分析，或給出魯棒濾波器。Riccati方程處理方法在80年代和90年代初期被廣大學者採用，對魯棒控制理論的發展起到了很大的促進作用。然而，隨著研究問題的日益複雜，越來越多的學者認識到Riccati方法的局限性：

1) Riccati型矩陣方程本身的求解存在一定的問題。目前有很多求解Riccati型矩陣方程的方法，但大多為疊代方法，這些方法的收斂性不能得到保證；

2)在套用Riccati方法進行不確定系統的分析和綜合時，往往需要設計者事先確定一些待定參數，這些參數的選擇不僅直接影響到結論的好壞，而且還會影響到問題的可解性。

但在現有的Riccati方程處理方法中，還缺乏尋找這些參數最佳值的方法，多數情況下尚需要人為的確定這些參數，無疑給分析和綜合結果引入了很大的保守性。

自從20世紀90年代初，線性矩陣不等式逐漸受到控制界的普遍關注，主要得益於求解凸最佳化問題的內點法的提出。在過去的十多年裡，線性矩陣不等式被廣泛套用到系統和控制的各個領域中。通過採用線性矩陣不等式技術，系統和控制中的很多問題可以轉化為一個線性矩陣不等式(組)的可行解問題，或者轉化為一個受線性矩陣不等式(組)約束的凸最佳化問題。內點法的提出使魯棒濾波分析和綜合中的一些原來無法解決的複雜問題在轉化為線性矩陣不等式問題後得以有效的解決。線性矩陣不等式方法可以克服Riccati方程處理方法中存在的許多不足。線上性矩陣不等式框架中研究不確定系統的魯棒分析和綜合問題時，所需要預先選擇的參數要明顯少於Riccati方法；線性矩陣不等式方法給出了問題解的一個凸約束條件，它一方面可以套用求解凸最佳化問題的有效方法來進行求解，另一方面，當求解這些約束條件時，所得到的可行解不是唯一的，而是一組滿足要求的可行解。因而可以對這一組解做進一步最佳化，這一點在多目標魯棒分析及綜合問題中具有明顯的優越性。線性矩陣不等式技術不僅為廣大科研工作者所採用，也正逐漸為工程師所接納。

隨機系統魯棒濾波

由於現代社會很多工程和經濟領域中的動態系統可抽象為隨機系統模型，這類系統在運行過程中常常受到外部環境和內部結構等隨機突變因素的影響。最近，一些學者己經開始對採用不確定模型描述的隨機系統，尤其是對隨機時滯系統的魯棒濾波問題展開研究，但對這一方面的研究還不是十分廣泛。

基本原理

魯棒濾波器的基本原理是：如果使系統干擾至系統誤差的傳遞函式矩陣的H∞範數最小，則具有有限功率譜的干擾對系統誤差的影響將會降到最低程度；或者是將噪聲看作能量有限的隨機信號，使系統干擾到估計誤差的閉環傳遞函式的H∞範數小於給定的正數。

研究方法

近十幾年，隨著不確定系統理論的發展，不確定系統的魯棒控制也取得了不同程度的發展。也提出了基於時域的魯棒濾波問題，將濾波器問題轉化為Riccati方程的求解問題。魯棒濾波是指考慮系統中的不確定性，設計濾波器使得濾波誤差系統漸近穩定，並且滿足所提出的性能指標。自從魯棒濾波方法被引入到系統的狀態估計中出現了大量的研究成果。如：

(1)魯棒H∞濾波。假設系統的噪聲輸入為能量有界信號，濾波器設計的主要依據是使濾波誤差系統的傳遞函式的H∞範數小於給定值；

(2)魯棒L2-L∞濾波。假設系統的噪聲輸入為能量有界信號，與H∞濾波的不同之處在於濾波器設計的主要依據是使濾波誤差系統具有一定的L2-L∞衰減水平，又稱為能量一峰值濾波；

(3)魯棒L1濾波。假定系統的噪聲輸入為峰值有界的信號，濾波器設計的主要依據是使相對於所有峰值有界的噪聲輸入信號，最劣情況下的濾波誤差信號的峰值小於給定值，又稱為峰值一峰值濾波。

具體構成

在的動態系統中，設系統噪聲與觀測噪聲為有限的能量信號，即：

則魯棒濾波就是設計一個濾波器，對於給定的正數γ，有：

上式滿足的充要條件是存在正定矩陣並滿足黎卡提(Riccati)方程，當γ趨於∞時，此時的魯棒濾波器就退化為卡爾曼濾波器。在實踐中，適當選擇γ值的大小，可使濾波誤差方差小並對不確定噪聲具有很好的魯棒性。

優點

在很多的工業套用中，系統中含有不確定參數，精確的系統模型是很難獲得的。因此，研究在模型存在不確定性下的濾波算法具有重要的理論意義，為了克服這個困難，魯棒濾波方法被引入，這個方法是考慮系統中的不確定性，設計濾波器使得濾波誤差系統漸近穩定，並且滿足所提的性能指標。魯棒濾波方法有如下優點：
(1)對系統的不確定性具有較強的魯棒性。
(2)與傳統的濾波方法相比較，魯棒濾波無需了解噪聲的特性。