高橋定理是子流形幾何的一個著名定理。
基本介紹
- 中文名:高橋定理
- 外文名:Takahashi theorem
高橋定理(Takahashi theorem)子流形幾何的一個著名定理.它是判斷歐氏空間中的子流形是否為某一超球面中的極小子流形.若x : MnR.R+‘為一等距浸人,乙表示M"的拉普拉斯運算元,則位置向量x滿足Ox=-.Lz,WO的充分必要條件是M”為__1,__,、___(幾),,._,_、一_,,,___一日‘甲‘甲的超壞臼(J'伙萬)甲的極小士侃憋·此i埋是由高橋健人發現的.由高橋定理,當M"是由它的乙的特徵函式等距浸人在歐氏空間中時M”是某個超球面中的極小子流形.例如,設(二,y,z)和(u‘ ,u ,... u)分別為R3和RS中的標準坐標系,考慮下面的映射:
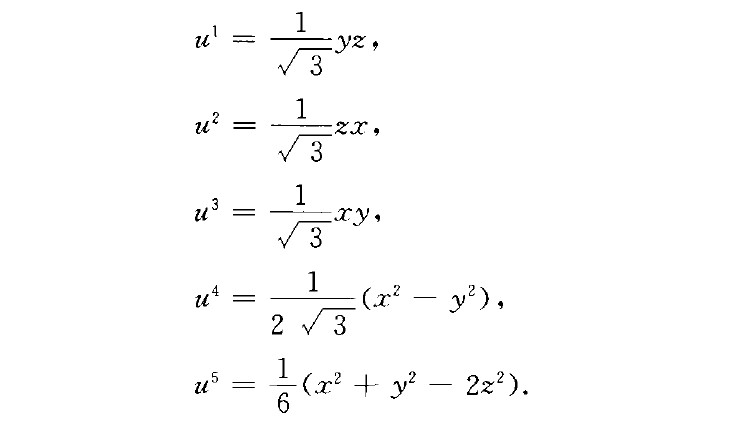
高橋定理
它是(S Z < /萬)到S`<1>的一等距浸人,(SZ < l萬)的兩點(x,y,z)和(-x,-y,-z)被映到541的同一點,上面的映射定義了從實射影空間R P' ( /萬)到S'(1)的一等距嵌人.從實射影空間的特徵函式理論有:Du`=-2u',i=1, 2,'''' , 5,所以由高橋定理知,它是S`(1)中的一極小曲面,稱為凡羅尼斯曲面.
