高斯-埃爾米特求積公式(Gauss-Hermite)是一種高斯型求積公式。
基本介紹
- 中文名：高斯—埃爾米特求積
- 外文名：Gauss-Hermite
- 適用領域：套用數學
指求積區間為（-∞，+∞），權函式
的正交多項式為埃爾米特多項式
高斯-埃爾米特求積公式
高斯-埃爾米特求積公式
相關詞條
- 高斯-埃爾米特求積公式
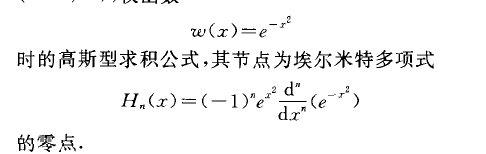
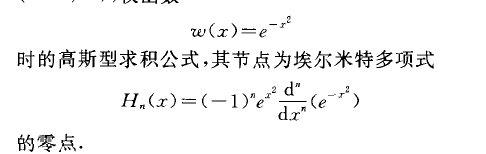
高斯-埃爾米特求積公式(Gauss-Hermite)是一種高斯型求積公式。指求積區間為（-∞，+∞），權函式的正交多項式為埃爾米特多項式對應的高斯型求積公式稱為高斯—埃爾米特求積公式。...
- 高等學校數學類規劃教材:數值計算方法
7.4.1 高斯求積公式與高斯點 7.4.2 高斯求積公式的構造 7.4.3 高斯一勒讓德求積公式 7.4.4 高斯一切比雪夫求積公式 7.4.5 高斯一埃爾米特求積公式 7.4.6 高斯求積公式的餘項及穩定性 7.5數值微分 7.5.1基於Taylor展式的微分公式 7.5.2插值型微分公式 本章小結 習題7 第8章常微分方程的數值...
- 數值分析(2008年清華大學出版社出版的圖書)
4.6 高斯求積公式(116)4.6.1 一般理論(116)4.6.2 高斯-勒讓德求積公式(121)4.6.3 高斯-切比雪夫求積公式(123)4.6.4 無窮區間的高斯型求積公式(124)4.7 多重積分(126)4.8 數值微分(128)4.8.1 中點方法與誤差分析(128)4.8.2 插值型的求導公式(130)4.8.3 三次樣條求導(132)4.8.4 數值...
- 科學計算引論:基於Mathematica的數值分析
6.1.2 牛頓-科茨求積公式 6.1.3 牛頓-科茨公式的誤差分析 6.2 復化求積公式 6.2.1 復化梯形求積公式 6.2.2 復化辛普森求積公式 6.2.3 事後誤差估計 6.3 外推原理與龍貝格求積法 6.3.1 外推原理 6.3.2 龍貝格求積法 6.4 高d斯求積公式 6.4.1 高斯求積公式的基本理論 6.4.2 常用高斯求積...
- 研究生系列教材:數值分析
3.1.4求積公式的收斂性與穩定性 3.2牛頓—柯特斯公式及餘項估計 3.2.1柯特斯係數 3.2.2偶數階求積公式的代數精度 3.2.3幾種低階求積公式的餘項 3.3復化求積法 3.3.1復化梯形公式 3.3.2復化辛普森公式 3.4龍貝格求積公式 3.4.1梯形法的遞推化 3.4.2龍貝格算法 3.5高斯求積公式 3.6數值微分...
- 數值分析與算法(2003年機械工業出版社出版的圖書)
7.4高斯求積法 7.4.1代數精度的概念 7.4.2高斯求積法 7.4.3幾種常用的高斯求積公式 7.5高振盪函式求積法 7.6數值微分 習題7第8章常微分方程數值解 8.1常微分方程數值解的基本思想 8.2歐拉方法 8.2.1基本公式 8.2.2誤差分析 8.2.3步長的自動選擇 8.2.4改進的歐拉公式 8.3龍格?庫塔法 8.4...
- 數值分析(第2版)(2018年科學出版社出版圖書)
5．5 埃爾米特插值 5．6 分段低次插值 5．7 三次樣條插值 5．8 部分算法程式 習題5 第6章 擬合 6．1 數據擬合 6．2 函式擬合 6．3 部分算法程式 習題6 第7章 數值積分 7．1 牛頓科茨求積公式 7．2 復化求積公式 7．3 龍貝格求積公式 7．4 高斯型求積公式 7．5 部分算法程式 習題7 第8章 常...
- MATLAB數值計算方法
5.7.3 龍貝格求積公式的MATLAB實現 5.8 高斯公式 5.8.1 高精度的求積公式 5.8.2 高斯點的基本特性 5.8.3 勒讓德多項式 5.8.4 高斯一勒讓德求積公式的MA'TLAB實現及套用實例 5.9 數值微分 第6章 常微分方程初值問題數值解法 6.1 求解常微分方程的MATLAB符號法 6.1.1 常微分方程的MATLAB符號表示...
- 數值計算方法(2020年科學出版社出版的圖書)
2.4埃爾米特插值 2.5分段低次插值 2.6樣條插值 2.7數值試驗2 習題2 第3章函式逼近與曲線擬合 3.1函式逼近的基本概念 3.2正交多項式 3.3最佳平方逼近 3.4曲線擬合的最小二乘法 3.5數值實驗3 習題3 第4章數值積分與數值微分 4.1數值積分的基本概念 4.2牛頓－科茨求積公式 4.3復化求積公式 4.4...
- 普通高等院校理工科教材:數值計算方法
2．3 差分及等距插值節點的牛頓插值公式 2．3．1 差分及其性質 2．3．2 牛頓前差和後差插值多項式 2．4 埃爾米特插值 2．4．1 三次埃爾米特插值 2．4．2 一般埃爾米特插值 2．5 構造埃爾米特插值函式的一般格式 2．6 分段低次插值和樣條插值 2．6．1 多項式插值的缺陷和分段低次插值 2．6．2 三次...
- 矩陣論與數值分析——理論及其工程套用
5.1.3 均差與牛頓插值公式 205 5.1.4 埃爾米特(Hermite)插值211 5.2 數值積分214 5.2.1 數值求積公式及代數精度215 5.2.2 插值型求積公式216 5.2.3 等距節點的求積公式217 5.2.4 復化求積公式219 5.2.5 龍貝格(Romberg)求積法222 5.2.6 高斯(Gauss)型求積公式227 5.3 數值微分231 5.3.1 ...
- 工程中的計算方法
4.3埃爾米特插值多項式 4.4三次樣條 4.5貝塞爾曲線 4.6插值的套用 4.7總結 練習題 第5章逼近 5.1最小二乘法 5.2函式內積 5.3最佳平方逼近 5.4切比雪夫多項式 5.5總結 練習題 第6章數值積分 6.1插值型求積公式 6.2變步長積分法 6.3求積公式的誤差 6.4收斂加速 6.5高斯型求積公式 6.6蒙特卡羅...
- 數值計算方法——人工智慧、大數據分析的數學基礎
3.5.2三點三次埃爾米特插值79 3.5.3分段三次埃爾米特插值80 3.6樣條插值81 3.6.1樣條函式81 3.6.2三次樣條插值83 習題387第4章疊代法89 4.1非線性方程求根89 4.1.1簡單疊代法90 4.1.2牛頓疊代法93 4.1.3弦截法95 4.2線性方程組的疊代解法97 4.2.1雅可比疊代法97 4.2.2高斯賽德爾疊代...
- 計算方法(第3版)
8.5 高斯求積公式 218 8.5.1 高斯點與高斯求積公式 218 8.5.2 高斯-勒讓德求積公式 219 8.5.3 高斯求積公式的穩定性和收斂性 222 8.6 數值微分 223 8.6.1 中點公式 223 8.6.2 插值型微分公式 225 8.7 算法實現 227 8.7.1 MATLAB編程實現 227 8.7.2 MATLAB函式實現 230 本章小結 233 習...
- 數值計算方法(2016年2月科學出版社出版的圖書)
5.3 差商與牛頓插值公式 137 5.4 差分與等距結點插值公式 140 5.5 埃爾米特插值 144 5.6 三次樣條插值 147 5.7 數值實驗 155 習題5 158 本章 常用辭彙中英文對照 159 第6章 數值積分與數值微分 160 6.1 引言 160 6.2 牛頓科茨公式 165 6.3 龍貝格算法 172 6.4 高斯求積公式 176 6.5 數值積分...
- 數值分析與方法
2.6 埃爾米特插值 2.7 分段低次插值 2.8 三次樣條插值 習題2 第3章 函式逼近與曲線擬合 3.1 函式逼近的基本概念 3.2 正交多項式 3.3 最佳平方逼近 3.4 曲線擬合的最小二乘法 習題3 第4章 數值微分與數值積分 4.1 數值微分 4.2 數值積分 4.3 等距節點求積公式 4.4 龍貝格求積公式 4.5 高斯...
- 高等數值計算
8.4.2變步長梯形公式 8.4.3理查森外推法 8.4.4龍貝格算法 8.5高斯求積公式 8.5.1高斯型求積公式的建立 8.5.2高斯求積公式的餘項 8.5.3高斯勒讓德求積公式 8.5.4高斯切比雪夫求積公式 8.6數值微分 8.6.1差商公式及誤差分析 8.6.2插值型求導公式 8.6.3三次樣條求導 習題8 第9章常微分...
- S數值計算方法
第四節 埃爾米特插值 第五節 分段低次插值 第六節 樣條插值 習題二 第三章 曲線擬合 第一節 最小二乘法 第二節 多項式曲線擬合 第三節 加權最小二乘法 第四節 正交多項式擬合 習題三 第四章 數值積分與數值微分 第一節 牛頓-柯特斯求積公式 第二節 復化求積公式 第三節 龍貝格求值公式 第四節 高斯型...
- 現代數值計算方法(第二版)
§4 差分與等距節點插值公式(124) 一、差分的定義與性質(124) 二、等距節點插值多項式及其餘項(126) *§5 埃爾米特插值(129) 一、一般情形的埃爾米特插值問題(129) 二、特殊情形的埃爾米特插值問題(131) *§6 三次樣條插值(132) 一、三次樣條插值函式的定義(133) 二、三次樣條插值函式的構造(133) 本章...
- 計算方法及其套用
§3.4高斯求積公式62 3.4.1一點高斯公式62 3.4.2二點高斯公式62 3.4.3n點高斯公式63 §3.5數值微分65 3.5.1差商與數值微分65 3.5.2插值型數值微分66 3.5.3樣條插值數值微分公式68 3.5.4上機程式68 §3.6上機實驗69 3.6.1實驗目的69 3.6.2實驗內容與要求69 3.6.3實驗題目70 習題71 第4...
- 數值分析(2014年科學出版社出版)
2.4 埃爾米特插值 2.5 分段低次插值 2.6 三次樣條插值 2.7 最小二乘擬合 習題二 第3章 數值積分 3.1 牛頓-柯特斯求積公式 3.2 復化求積公式 3.3 龍貝格公式 3.4 高斯型求積公式 習題三 第4章 解線性方程組的直接法 4.1 高斯消去法 4.2 矩陣的LU分解法 4.3 特殊線性方程組的三角分解法 4...
- 計算方法及其套用(高等學校計算機套用規劃教材)
§3.4高斯求積公式62 3.4.1一點高斯公式62 3.4.2二點高斯公式62 3.4.3n點高斯公式63 §3.5數值微分65 3.5.1差商與數值微分65 3.5.2插值型數值微分66 3.5.3樣條插值數值微分公式68 3.5.4上機程式68 §3.6上機實驗69 3.6.1實驗目的69 3.6.2實驗內容與要求69 3.6.3實驗題目70 習題71 第4...
- 工程數學數值分析與矩陣論(上冊)
6.4 埃爾米特插值 6.5 三次樣條插值 6.6 B-樣條函式 6.7 正交多項式 6.8 最佳平方逼近 6.9 曲線擬合的最小二乘法 第七章 數值積分 7.1 數值積分概述 7.2 牛頓－柯特斯求積公式 7.3 自適應積分法 7.4 龍貝格求積算法 7.5 高斯求積方法 第八章 常微分方程初值問題的數值解法 8.1 ...
- 數值分析簡明教程
例題選講1．4 牛頓插值公式 47 例題選講1．5 埃爾米特插值 50 習題一 54 第二章 數值積分 58 2．1 機械求積 58 2．2 牛頓-柯特斯公式 61 2．3 龍貝格算法 66 2．4 高斯公式 71 2．5 數值微分 76 例題選講2．1 機械求積 80 例題選講2．2 求積公式的設計 81 例題選講2．3 高斯求積公式 86 ...
- 數值分析(2005年清華大學出版社出版的圖書)
7. 3. 2 復化辛普生公式 7. 4 龍貝格積分法 7. 4. 1 區間逐次分半法 7. 4. 2 龍貝格積分法 7. 5 高斯求積公式 7. 6 數值微分 7. 6. 1 兩點公式 7. 6. 2 三點公式 7. 6. 3 五點公式 習題 第8章 矩陣的特徵值與特徵向量的計算 8. 1 引言 8. 2 冪法. 反冪法 8. 2. 1 冪法 ...
- 數值計算方法(2007年上海大學出版社出版的圖書)
6 埃爾米特(Hermite)插值 7 多元函式插值 習題 第七章 小二乘逼近 1 引言 2 曲線擬合的小二乘法 3 函式逼近和正交多項式 習題 第八章 數值微分和數值積分 1 引言 2 數值微分 3 牛頓一柯特斯(Newton-Cotes)公式 4 複合求積公式 5 龍貝格(RorrLberg)方法 6 高斯(Gauss)型積分公式 7 關於數值積分的進一步...
- 計算方法(2020年人民郵電出版社出版的圖書)
6．4 高斯型求積公式 154 6．4．1 高斯型求積公式 154 6．4．2 正交多項式 155 6．4．3 高斯-勒讓德求積公式 156 6．5 實驗——廣義積分的數值求解 158 6．6 延伸閱讀 160 6．7 思考題 160 6．8 習題 160 6．9 實驗題 161 第7章 常微分方程初值問題的數值解 162 7．1 引入...
- 數值分析(研究生)
3.5 高斯求積公式 97 3.6 數值微分 101 3.7 數字圖像的導數與梯度 104 3.7.1 二維數據的一階導數 104 3.7.2 二維數據的二階導數 105 習題3 106 第4章 解線性方程組的方法 108 4.1 方程組的性態及條件數 108 4.2 高斯消去法和列主元消去法 111 4.2.1 高斯消去法 112 4.2.2 列主元消去...
- 數值計算方法(第3版)(機械工業出版社出版的圖書)
6.2.3梯形公式和辛普森公式的餘項207 6.2.4牛頓-柯特斯公式的穩定性210 6.3復化求積法212 6.3.1復化梯形公式212 6.3.2復化辛普森公式213 6.3.3復化柯特斯公式214 6.4變步長求積和龍貝格算法215 6.4.1變步長梯形求積法215 6.4.2龍貝格算法217 6.5高斯型求積公式219 6.5.1概述219 6.5.2高斯-...
- 科學和工程計算基礎
5.2.1 梯形公式和Simpson公式 164 5.2.2 復化梯形公式和復化Simpson公式 167 5.3 Gauss求積公式 170 5.3.1 Gauss點與正交多項式零點的關係 171 5.3.2 常用的Gauss型求積公式 173 5.3.3 Gauss公式的餘項 178 5.3.4 Gauss求積公式的數值穩定性和收斂性 179 5.4 數值微分 180 5.4.1 Taylor展開法 ...
