風荷載

風荷載（wind load） 空氣流動對工程結構所產生的壓力。其大小與風速的平方成正比，即

式中ρ為空氣品質密度，va和vb分別為風法結構表面前與結構表面後的風速。

基本介紹

• 中文名：風荷載
• 外文名：wind load

基本含義

風荷載也稱風的動壓力，是空氣流動對工程結構所產生的壓力。風荷載ш與基本風壓、地形、地面粗糙度、距離地面高度，及建築體型等諸因素有關。中國的地理位置和氣候條件造成的大風為：夏季東南沿海多颱風，內陸多雷暴及雹線大風；冬季北部地區多寒潮大風，其中沿海地區的颱風往往是設計工程結構的主要控制荷載。颱風造成的風災事故較多，影響範圍也較大。雷暴大風可能引起小範圍內的風災事故。

風荷載

計算公式

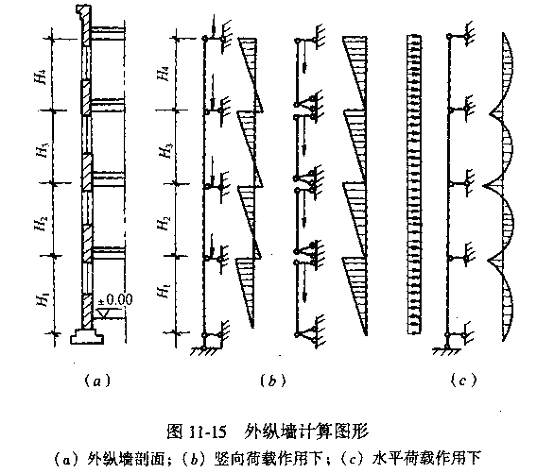
垂直於建築物表面上的風荷載標準值，應按下述公式計算：

1 當計算主要承重結構時,按式：wk=βzμsμzWo

式中wk—風荷載標準值(kN/m2)；

βz—高度z 處的風振係數；

μs—風荷載體型係數；

μz—風壓高度變化係數；

Wo—基本風壓(kN/㎡)。

2 當計算圍護結構時，按式：wk=βgzμslμzWo

式中βgz—高度z 處的陣風係數；

μsl--風荷載局部體型係數。

風荷載參數

基本風壓

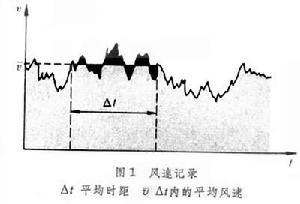
中國規定的基本風壓w0 以一般空曠平坦地面、離地面10米高、風速時距為10分鐘平均的最大風速為標準，按結構類別考慮重現期(一般結構重現期為30年，高層建築和高聳結構為50年,特別重要的結構為100年),統計得最大風速v（即年最大風速分布的96.67%分位值，並按w0=ρv2/2確定。式中ρ為空氣品質密度；v為風速）。根據統計，認為離地面10米高、時距為10分鐘平均的年最大風壓，統計分布可按極值I型考慮。　基本風壓因地而異，在中國的分布情況是：台灣和海南島等沿海島嶼、東南沿海是最大風壓區，由颱風造成。東北、華北、西北的北部是風壓次大區，主要與強冷氣活動相聯繫。青藏高原為風壓較大區，主要由海拔高度較高所造成。其他內陸地區風壓都較小。　風速 　風速隨時間不斷變化（圖1）,在一定的時距Δt內將風速分解為兩部分：一部分是平均風速的穩定部分；另一部分是指風速的脈動部分。為了對變化的風速確定其代表值作為基本風壓，一般用規定時距內風速的穩定部分作為取值標準。

風荷載

建築設計中的取用：基本風壓應按《建築結構荷載規範》附錄D.4 中附表D.4 給出的50 年一遇的風壓採用，但不得小於0.3kN/m2。

對於高層建築、高聳結構以及對風荷載比較敏感的其他結構，基本風壓應適當提高，並應由有關的結構設計規範具體規定。

當城市或建設地點的基本風壓值在本規範全國基本風壓圖上沒有給出時，基本風壓值可根據當地年最大風速資料，按基本風壓定義，通過統計分析確定,分析時應考慮樣本數量的影響(參見附錄D)。當地沒有風速資料時，可根據附近地區規定的基本風壓或長期資料，通過氣象和地形條件的對比分析確定；也可按本規範附錄D中全國基本風壓分布圖(附圖D.5.3)近似確定。

風荷載的組合值、頻遇值和準永久值係數可分別取0.6、0.4 和0。

平均時距

按風速記錄為確定最大平均風速而規定的時間間隔（圖1）。規定的時距愈短，所得的最大平均風速愈大，也即基本風壓愈大。當前世界各國所採用的平均時距標準並不一致，例如，中國時距取10分鐘,蘇聯取2分鐘，英國根據建築物或構件的尺寸不同，分別取3秒、5秒和15秒，日本取瞬時。美國以風程1609.3米（1英里）作為確定平均風速的標準，這相當於對不同風速取不同的平均時距。因而各國基本風壓值的標準也有差別。

風壓高度變化係數

從某一高度的已知風壓（如高度為10米的基本風壓），推算另一任意高度風壓的係數。風壓高度變化係數隨離地面高度增加而增大，其變化規律與地面粗糙度及風速廓線直接有關。設計工程結構時應在不同高度處取用對應高度的風壓值。

風荷載

對於平坦或稍有起伏的地形，風壓高度變化係數應根據地面粗糙度類別按表8.2.1 確定。

地面粗糙度可分為A、B、C、D 四類：

——A 類指近海海面和海島、海岸、湖岸及沙漠地區；

——B 類指田野、鄉村、叢林、丘陵以及房屋比較稀疏的鄉鎮和城市郊區；

——C 類指有密集建築群的城市市區；

——D 類指有密集建築群且房屋較高的城市市區。

1. 8.2.2對於山區的建築物，風壓高度變化係數可按平坦地面的粗糙度類別，由表8.2.1確定外，還應考慮地形條件的修正，修正係數η分別按下述規定採用:

1 對於山峰和山坡，其頂部B 處的修正係數可按下述公式採用：

式中tg α—山峰或山坡在迎風面一側的坡度；當tg α>0.3 時，取tg α=0.3；

k—係數，對山峰取3.2，對山坡取1.4；

H—山頂或山坡全高(m)；

z—建築物計算位置離建築物地面的高度，m；當z>2.5H 時，取z=2.5H。

對於山峰和山坡的其他部位，可按圖8.2.2 所示，取A、C 處的修正係數ηA、ηC 為1，AB 間和BC 間的修正係數按η的線性插值確定。

2 山間盆地、谷地等閉塞地形η=0.75～0.85；

對於與風向一致的谷口、山口η=1.20～1.50。

1. 8.2.3對於遠海海面和海島的建築物或構築物，風壓高度變化係數可按A 類粗糙度類別，由表8.2.1 確定外，還應考慮表8.2.3 中給出的修正係數。

地面粗糙度

地面因障礙物形成影響風速的粗糙程度。風（氣流）在接近地面運動時，受到樹木、房屋等障礙物的摩擦影響，消耗了一部分動能，使風速逐漸降低。這種影響一般用地面粗糙度衡量。地面粗糙度愈大，同一高度處的風速減弱愈顯著。一般地面粗糙度可由小而大列為水面、沙漠、空曠平原、灌木、村、鎮、丘陵、森林、大城市等幾類。

風速廓線

風速隨高度的變化曲線(圖2)。風速通常隨離地面高度增大而增加。增加程度主要與地面粗糙度和溫度梯度有關。達到一定高度後，地面的摩擦影響可忽略不計，該高度稱為梯度風高度。梯度風高度隨地面粗糙度而異,一般約為300～500 米。梯度風高度以內的風速廓線一般可用指數曲線表示。

風載體型係數

也稱空氣動力係數，它是風在工程結構表面形成的壓力（或吸力）與按來流風速算出的理論風壓的比值。它反映出穩定風壓在工程結構及建築物表面上的分布，並隨建築物形狀、尺度、圍護和禁止狀況以及氣流方向等而異。對尺度很大的工程結構及建築物，有可能並非全部迎風面同時承受最大風壓。對一個建築物而言，從風載體型係數得到的反映是：迎風面為壓力；背風面及順風向的側面為吸力；頂面則隨坡角大小可能為壓力或吸力。

風荷載

1. 8.3.1房屋和構築物的風載體型係數，可按下列規定採用:

1 房屋和構築物與表8.3.1 中的體型類同時，可按該表的規定採用；

2 房屋和構築物與表8.3.1 中的體型不同時，可參考有關資料採用；

3 房屋和構築物與表8.3.1 中的體型不同且無參考資料可以借鑑時，宜由風洞試驗確定；

4 對於重要且體型複雜的房屋和構築物，應由風洞試驗確定。

1. 8.3.2當多個建築物，特別是群集的高層建築，相互間距較近時，宜考慮風力相互干擾的群體效應；一般可將單獨建築物的體型係數μs乘以相互干擾增大係數，該係數可參考類似條件的試驗資料確定；必要時宜通過風洞試驗得出。
2. 8.3.3驗算圍護構件及其連線的強度時，可按下列規定採用局部風壓體型係數:
3. 一、外表面

1 正壓區按表8.3.1 採用；

2 負壓區

－對牆面，取-1.0；

－對牆角邊，取-1.8；

－對屋面局部部位(周邊和屋面坡度大於10°的屋脊部位)，取-2.2；

－對檐口、雨篷、遮陽板等突出構件，取-2.0。

注:對牆角邊和屋面局部部位的作用寬度為房屋寬度的0.1 或房屋平均高度的0.4，取其小者，但不小於1.5m。

1. 內表面

對封閉式建築物，按外表面風壓的正負情況取-0.2 或0.2。

風振

風的脈動部分對高聳結構所引起的動態作用。一般結構對風力的動態作用並不敏感，可僅考慮靜態作用。但對於高聳結構（如塔架、煙囪、水塔）和高層建築，除考慮靜態作用外，還需考慮動態作用。動態作用與結構自振周期、結構振型，結構阻尼和結構高度等因素有關，可將脈動風壓假定為各態歷經隨機過程按隨機振動理論的基本原理導出。為方便起見，動態作用常用等效靜態放大係數，即風振係數的方式與靜態作用一併考慮。

1. 8.4.1對於基本自振周期T1 大於0.25s 的工程結構，如房屋、屋蓋及各種高聳結構,以及對於高度大於30m 且高寬比大於1.5 的高柔房屋，均應考慮風壓脈動對結構發 生順風向風振的影響。風振計算應按隨機振動理論進行，結構的自振周期應按結構動力學計算。

注:近似的基本自振周期T1 可按附錄E 計算。

1. 8.4.2對於一般懸臂型結構，例如構架、塔架、煙囪等高聳結構,以及高度大於30m，高寬比大於1.5 且可忽略扭轉影響的高層建築，均可僅考慮第一振型的影響，結構的風荷載可按公式(8.1.1-1)通過風振係數來計算，結構在z 高度處的風振係數βz 可按下式計算:

式中ξ—脈動增大係數；

υ—脈動影響係數；

—振型係數；

μz—風壓高度變化係數。

1. 8.4.3脈動增大係數，可按表8.4.3 確定。

註：計算 時，對地面粗糙度B 類地區可直接代入基本風壓，而對A 類、C 類和D 類地區應按當地的基本風壓分別乘以1.38、0.62 和0.32 後代入。

1. 8.4.4脈動影響係數，可按下列情況分別確定。

1 結構迎風面寬度遠小於其高度的情況(如高聳結構等)：

1. 若外形、質量沿高度比較均勻，脈動係數可按表8.4.4-1 確定。
2. 當結構迎風面和側風面的寬度沿高度按直線或接近直線變化，而質量沿高度按連續規律變化時，表8.4.4-1 中的脈動影響係數應再乘以修正係數θB 和θv。θB應為構築物迎風面在z 高度處的寬度Bz 與底部寬度B0 的比值； θν可按表8.4.4-2 確定。

2 結構迎風面寬度較大時,應考慮寬度方向風壓空間相關性的情況(如高層建築等):若外形、質量沿高度比較均勻，脈動影響係數可根據總高度H 及其與迎風面寬度B 的比值，按表8.4.4-3 確定。

8.4.5振型係數應根據結構動力計算確定。對外形、質量、剛度沿高度按連續規律變化的懸臂型高聳結構及沿高度比較均勻的高層建築,振型係數也可根據相對高度z/H 按附錄F 確定。

8.5.1對矩形截面高層建築當滿足下列條件時，確定其橫風向風振等效風荷載：

1 建築的平面形狀和質量在整個高度範圍內基本相同;
2 高寬比HμBD在4~8 之間，深寬比D/B 在o. 5~2 之
間，其中B 為結構的迎風面寬度.D 為結構平面的進深(順風向尺寸) ;間，其中B 為結構的迎風面寬度.D 為結構平面的進深(順風向尺寸) ;
3 vHTu //西運10. Tu 為結構橫風向第1 階自振周期，均為結構頂部風速。

8.6.1對圓形截面的結構，應根據雷諾數Re 的不同情況按下述規定進行橫風向風振(旋渦脫落)的校核：

1 當Re<3×10 時(亞臨界的微風共振)，應按下式控制結構頂部風速υH 不超過臨界風速υcr， υcr 和υH 可按下列公式確定：

式中T1—結構基本自振周期；

St—斯脫羅哈數，對圓截面結構取0.2；

γW—風荷載分項係數，取1.4；

μH—結構頂部風壓高度變化係數；

ω0—基本風壓(kN/m)；

ρ—空氣密度(kg/m)。

當結構頂部風速超過υcr 時，可在構造上採取防振措施，或控制結構的臨界風速υcr 不小於15m/s。

2 Re≥3.5×10且結構頂部風速大於υcr 時(跨臨界的強風共振)，應按第8.6.2條考慮橫風向風荷載引起的荷載效應。

3 雷諾數Re 可按下列公式確定：

Re=69000vD (8.6.1-3)

式中υ—計算高度處的風速(m/s)；

D—結構截面的直徑(m)。

4 當結構沿高度截面縮小時(傾斜度不大於0.02)，可近似取2/3 結構高度處的風速和直徑。

1. 8.6.2跨臨界強風共振引起在z 高處振型j 的等效風荷載可由下列公式確定：

式中 —計算係數，按表8.6.2 確定；

—在z 高處結構的j 振型係數，由計算確定或參考附錄F；

ζj—第j 振型的阻尼比；對第1 振型，鋼結構取0.01，房屋鋼結構取0.02，

混凝土結構取0.05；對高振型的阻尼比，若無實測資料，可近似按第1 振型的值取用。

表8.6.2 中的H1 為臨界風速起始點高度，可按下式確定：

式中α—地面粗糙度指數，對A、B、C 和D 四類分別取0.12、0.16、0.22 和0.30；

υH—結構頂部風速(m/s)。

注:校核橫風向風振時所考慮的高振型序號不大於4，對一般懸臂型結構，可只取第1 或第2 個振型。

1. 8.6.3校核橫風向風振時，風的荷載總效應可將橫風向風荷載效應Sc 與順風向風荷載效應SA 按下式組合後確定：
2. 8.6.4對非圓形截面的結構，橫風向風振的等效風荷載宜通過空氣彈性模型的風洞試驗確定；也可參考有關資料確定。
   膜結構中的風荷載

風荷載是膜結構設計控制荷載之一，一般作為靜荷載進行結構分析。組合值為0 6、頻遇值為0 4、準永久值係數為O。

風振係數，指將lOmin平均風壓係數轉化為瞬時風壓係數，同時考慮風荷載脈動與結構動力之間的諧振效應。風振係數不僅與建築場地有關，且與結構自振特性有關，很難給出“準確值”c大型空間結構屬柔性結構體系，自振頻率小，振形密集，以至存在大量同頻率振形，振形間模態相關性強。對動力效應起作用的頻率多，且低階振形並不一定為主振形，某些高階振形動力效應反而大。因此，不能用低階或某階振形頻率確定風振係數，需要綜合評價結構整體動力特性，結合既往相似工程，選取合理值。

陣風係數

1. 8.5.1計算圍護結構風荷載時的陣風係數應按表8.5.1 確定。