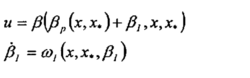非線性狀態PI控制

隨著非線性控制理論研究的深入，非線性不確定系統的控制成為控制界的研究熱點之一。

非線性狀態PI控制(The nonlinear State PI control 是一種新型的控制方法，它摒棄了傳統自適應控制採用的參數辨識加反饋控制器設計的結構，將系統的動態表達成期望動態特性加擾動項的形式，在不知道非線性不確定函式具體形式的情況下，通過確定該函式的界來設計控制器的參數，使系統能夠達到期望動態特性。

基本介紹

• 中文名：非線性狀態PI控制
• 外文名：The nonlinear State PI control
• 涉及學科：信息科學
• 套用：自動化
• 作用對象：非線性系統
• 表達成：動態特性加擾動項

簡介

在生產生活的各個領域中許多系統都存在著或多或少的不確定因素，然而為了簡化控制器設計的複雜程度，往往在對這些系統進行建模的過程中忽略了這些不確定的因素，因此系統的動態性能要受到一定程度的影響，甚至有時會出現不穩定的情況。例如在對飛機進行控制器的設計時，飛機在飛行的過程中會受到風速，氣壓，溫度等很多不確定因素的影響，而這些因素如果不被考慮到控制器的設計中，很有可能引起飛行的失敗，造成生命和財產的損失。因此自動控制技術面臨一個很重要的課題，即在被控對象含有某種不確定性的前提下，如何設計控制器使系統儘可能接近或者達到理想的控制指標。上述問題就是通常所說的魯棒控制問題，隨著控制理論的發展，非線性狀態PI控制也屬於魯棒控制的一種。

隨著非線性控制理論研究的深入，非線性不確定系統的控制成為控制界的研究熱點之一。非線性狀態PI控制是一種新型的控制方法，它摒棄了傳統自適應控制採用的參數辨識加反饋控制器設計的結構，將系統的動態表達成期望動態特性加擾動項的形式，在不知道非線性不確定函式具體形式的情況下，通過確定該函式的界來設計控制器的參數，使系統能夠達到期望動態特性。

優勢

非線性狀態PI控制方法是一種適用於控制線性系統和非線性系統的方法，尤其適用於對不確定系統進行控制，與自適應控制方法的不同之處在於該方法不需要對未知的參數進行辨識。在對包含非線性不確定項的系統進行控制時，如果採用自適應控制算法，必須對非線性參數化的未知項進行辨識，然後根據確定性等效原理和李亞普諾夫穩定性理論推出控制器。然而對非線性參數化的未知項進行辨識是比較困難的，大多數方法都是建立在對非線性函式特性的某些幾何假設的基礎上，並不能廣泛套用。如果利用反饋線性化或其他方法將該非線性不確定項轉化成為線性參數化的形式，將可能導致由於超參數化造成的系統階數的增加和不穩定的零極點對消等消極因素。非線性狀態PI控制方法彌補了自適應控制在這方面的不足，它首先將系統表達成期望動態特性加擾動項的形式，通過了解非線性不確定項的界來設計非線性狀態PI控制器參數，在控制器的作用下隨著擾動項漸近趨於零，使系統能夠漸近達到期望的動態特性，從而實現控制目的。

定義

首先給出非線性狀態PI控制器的定義：對於可測信號

，參考信號

和標量控制信號，定義如下三個映射：

通過下面的式子可以構成非線性狀態PI控制器

式中，和分別為非線性比例係數和微分係數。

事實上，從上面的定義可以立即推出下面的結論：經典的單輸入單輸出線性PI控制器是非線性狀態PI控制器的特例，圖1為單輸入單輸出線性PI控制器。

圖1 單輸入單輸出線性PI控制器

原理

採用一個簡單的例子說明非線性狀態PI控制器的設計原理。假設需要控制的對象為包含有界非線性不確定項的一階系統：

式中x表示系統狀態，u表示控制輸入，a為已知參數， 為關於x的非線性函式，其參數和具體形式不知道，只知道它的界。控制目標是設計控制輸入u，使得 。為了實現控制目標，設期望動態特性為量

，可以看出，如果系統能夠達到期望動態特性，則狀態x可以指數收斂到零。

系統表達成期望動態特性加擾動項的形式：

若存在 ，使得對於每一個x值，擾動項：

並且 漸近收斂於z，則系統能夠漸近達到期望的動態特性。

所以得出結論：如果z存在穩定的平衡點，則擾動項能夠漸近趨於零。為了考察z是否存在穩定的平衡點，將z的動態特性看成關於z的系統，將x視為參數，可以證明，對於所有的x，存在充分大的正整數N，有：

在該控制器的作用下，系統能夠在有限的時間內收斂到該區域。

比較

自適應控制是也是一種控制方法，對於通常形式的 ，當用非線性參數化逼近時，自適應控制是無能為力的；當使用線性參數化逼近時，為了保證逼近的精度，就必須增加未知參數的個數，從而導致系統實際維數的增加，影響了系統的動態性能。

而非線性狀態PI控制方法不需要對未知的非線性函式進行參數化，實際上也避免了參數估計問題，它通過設計非線性狀態PI控制器及其參數，調解系統逐漸達到期望的動態特性，是解決這類問題的比較好的方法。