非直謂定義法

非直謂定義法(the method of impredicative definition)是一種下定義的方法，指被定義的對象被包括在藉以定義它的各個對象之中的定義方法，亦即“藉助於一個總體來定義一個概念，而這個概念本身又屬於這一總體”。例如：自然數全體N中最小的那個自然數0；一切序數組成的良序集W的序數β；一切良序集所組成的良序集θ；一切集合所組成的集合E等。龐加萊((J.-)H.Poincaré)曾在1905年、1906年和1908年多次指出，所有的悖論都與非直謂定義有關。

基本介紹

• 中文名：非直謂定義法
• 外文名：the method of impredicative definition
• 所屬學科：數學
• 相關人物：龐加萊((J.-)H.Poincaré)
• 屬性：一種下定義的方法

舉例

關於悖論的成因，Poincaré曾在1905、1906、1908年多次指出。所有的悖論都與非直謂定義有關。何謂非直謂定義?就是“被定義的對象被包括在藉以定義它的各個對象中"。說得更明確一點，就是“藉助於一個總體來定義一個概念，而這個概念本身又屬於這一總體”。舉例如下：

例1 自然數全體N中最小的那個自然數1。

在這裡被定義的對象是自然數“1”，但藉以定義“1"的概念是“最小”和“自然數全體N”，但在定義“自然數全體N”時，首先要藉助於每個自然數，其中包括“1"這個自然數在內，這就是藉助於總體N來定義1，而1本身又屬於總體N。

例2 李家莊村上年紀最大的人H。

這裡被定義的對象是H這個人，但當我們對H下定義時，一方面藉助了“年紀最大”的概念，特別是藉助了“李家莊村上所有的人所組成的總體G”這一概念，但要定義總體G的話，又要藉助李家莊村上每一個人，其中包括H這個人在內，這就是藉助於總體G來定義H，而H本身又屬於總體G。如圖1所示。

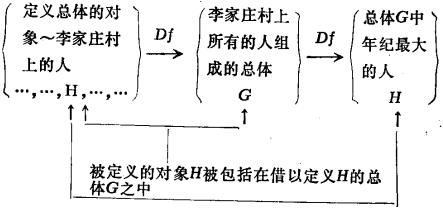
圖1

例3 一切序數所組成的良序集W的序數 。

如圖2所示。

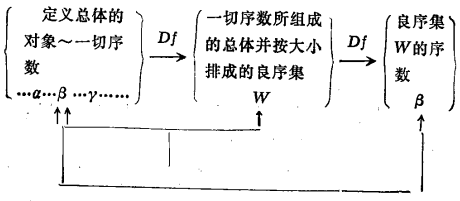
圖2

例4 一切正序集所組成的良序集 。

每一良序集對應於一個序數，故把一切良序集匯成總體後，再按每一良序集所對應的序數的大小為次序把這個總體排成良序集 ，如圖3所示。

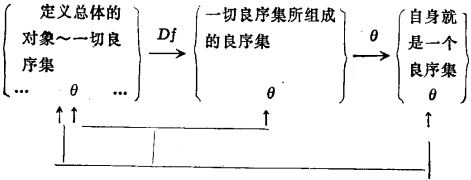
圖3

例5 一切集合所組成的集合。

如圖4所示。

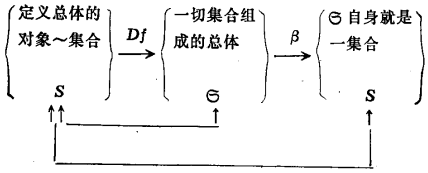
圖4

分類

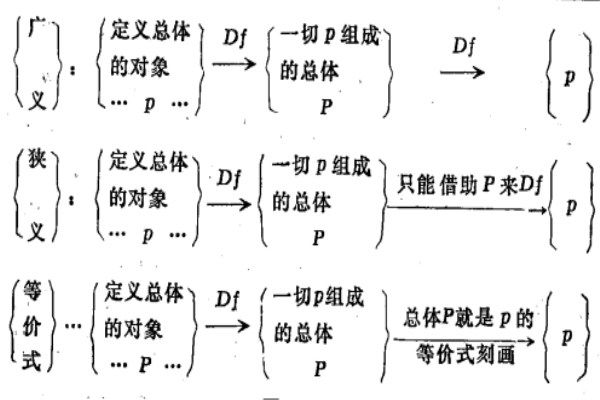
以上五例都是非直謂定義法，但它們構成非直謂定義的具體過程卻有所不同，按其不同的情況可作如下的分類：

廣義

凡是非直謂定義中的被定義對象，可用直謂定義法重新定義者，亦即被定義的對象並非只能藉助於包括它的總體來加以定義者叫做廣義非直謂。如例1中的自然數“1"，既可藉助於N來定義，也可不藉助於N而用直謂定義法重新定義。又如例2中的H，既可藉助於G來定義，也可用“李大娘的老伴"、“王小二的祖父"等等直謂地定義H。

狹義

凡是非直謂定義中的被定義對象非藉助於總體不可，亦即被定義的對象只能藉助於這一總體才能定義，如例3中的序數 。由於序數 就是良序集W的序數 ，如果丟開總體W，如何來講W的序數呢?亦即因為 是W的 ，不是別的 ，那么 就只能藉助於W來定義它了。又看例2，構想有一個不是李家莊村上的外地人K，並且K對李家莊村上的人和事一無所知，現在K要到李家莊村上找年紀最大的人H了解一件事，那么K到李家莊後，如何向李家莊村上的人來表達“他要找H問事"這個意思呢?在此時此刻對這個特定的人K來說，就非藉助於總體G來向別人詢找H這個人了。因此，例2本來是廣義非直謂，但廣義非直謂之下的這個H相對於特定條件下的特定的K而言，就成為狹義非直謂之下的H了。

等價式

凡是非直謂定義中的被定義對象僅藉助於“總體本身就是什麼”這樣的等價式刻畫來確定的，則稱為等價式的非直謂。如例4中的被定義對象就是通過“ 本身就是一個良序集"這樣的等價式刻畫來確定的。例5中的被定義對象也是通過“一切集合的集合就是一個集合"這種自身等於自己的方式來刻畫的。如果把這種等價式的刻畫亦算作一種自相的定義方式的話，當然也須納入非藉助於總體定義的情形中去，因此，等價式非直謂是狹義非直謂的特殊情形，而狹義非直謂又是廣義非直謂的特殊情形。如用記號“A B”來表示A是B的特殊情形，那么三種非直謂定義法的關係是：

等價式非直謂 狹義非直謂 廣義非直謂

綜上所述，可將三種非直謂圖示如圖5（a）-圖5（c）：

圖5（a）

圖5（b）

圖5（c）

以上關於非直謂定義法的分析討論，亦即關於它們的分類和各類非直謂之間的關係，對於我們了解悖論的成因和尋找排除悖論的出路有密切的關係。