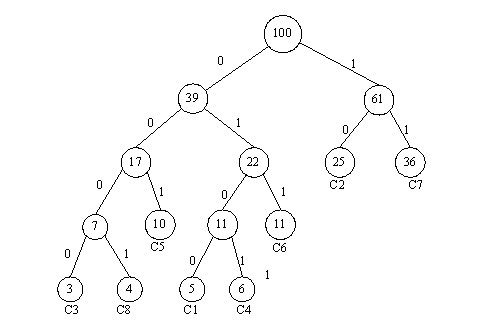
給定N個權值作為N個?>葉子結點,構造一棵二叉樹,若該樹的帶權路徑長度達到最小,稱這樣的二叉樹為最優二叉樹,也稱為哈夫曼樹(Huffman Tree)。哈夫曼樹是帶權路徑長度最短的樹,權值較大的結點離根較近。
基本介紹
- 中文名:哈夫曼樹
- 外文名:Huffman Tree
- 又名:最優樹
- 路徑長度:根結點到第L層結點路徑長度為L-1
- 帶權路徑長度:WPL
- 套用:哈夫曼編碼
簡介,歷史,套用,基本術語,構造,多叉哈夫曼樹,實現方法,數據壓縮,數據解壓縮,示例,
簡介
在計算機數據處理中,哈夫曼編碼使用變長編碼表對源符號(如檔案中的一個字母)進行編碼,其中變長編碼表是通過一種評估來源符號出現機率的方法得到的,出現機率高的字母使用較短的編碼,反之出現機率低的則使用較長的編碼,這便使編碼之後的字元串的平均長度、期望值降低,從而達到無損壓縮數據的目的。
例如,在英文中,e的出現機率最高,而z的出現機率則最低。當利用哈夫曼編碼對一篇英文進行壓縮時,e極有可能用一個比特來表示,而z則可能花去25個比特(不是26)。用普通的表示方法時,每個英文字母均占用一個位元組,即8個比特。二者相比,e使用了一般編碼的1/8的長度,z則使用了3倍多。倘若我們能實現對於英文中各個字母出現機率的較準確的估算,就可以大幅度提高無損壓縮的比例。
哈夫曼樹又稱最優二叉樹,是一種帶權路徑長度最短的二叉樹。所謂樹的帶權路徑長度,就是樹中所有的葉結點的權值乘上其到根結點的路徑長度(若根結點為0層,葉結點到根結點的路徑長度為葉結點的層數)。樹的路徑長度是從樹根到每一結點的路徑長度之和,記為WPL=(W1*L1+W2*L2+W3*L3+...+Wn*Ln),N個權值Wi(i=1,2,...n)構成一棵有N個葉結點的二叉樹,相應的葉結點的路徑長度為Li(i=1,2,...n)。可以證明哈夫曼樹的WPL是最小的。
歷史
1951年,哈夫曼在麻省理工學院(MIT)攻讀博士學位,他和修讀資訊理論課程的同學得選擇是完成學期報告還是期末考試。導師羅伯特·法諾(Robert Fano)出的學期報告題目是:查找最有效的二進制編碼。由於無法證明哪個已有編碼是最有效的,哈夫曼放棄對已有編碼的研究,轉向新的探索,最終發現了基於有序頻率二叉樹編碼的想法,並很快證明了這個方法是最有效的。哈夫曼使用自底向上的方法構建二叉樹,避免了次優算法香農-范諾編碼(Shannon–Fano coding)的最大弊端──自頂向下構建樹。
1952年,於論文《一種構建極小多餘編碼的方法》(A Method for the Construction of Minimum-Redundancy Codes)中發表了這個編碼方法。
套用
1、哈夫曼編碼
在數據通信中,需要將傳送的文字轉換成二進制的字元串,用0,1碼的不同排列來表示字元。例如,需傳送的報文為“AFTER DATA EAR ARE ART AREA”,這裡用到的字元集為“A,E,R,T,F,D”,各字母出現的次數為{8,4,5,3,1,1}。現要求為這些字母設計編碼。要區別6個字母,最簡單的二進制編碼方式是等長編碼,固定採用3位二進制,可分別用000、001、010、011、100、101對“A,E,R,T,F,D”進行編碼傳送,當對方接收報文時再按照三位一分進行解碼。顯然編碼的長度取決報文中不同字元的個數。若報文中可能出現26個不同字元,則固定編碼長度為5。然而,傳送報文時總是希望總長度儘可能短。在實際套用中,各個字元的出現頻度或使用次數是不相同的,如A、B、C的使用頻率遠遠高於X、Y、Z,自然會想到設計編碼時,讓使用頻率高的用短碼,使用頻率低的用長碼,以最佳化整個報文編碼。
為使不等長編碼為前綴編碼(即要求一個字元的編碼不能是另一個字元編碼的前綴),可用字元集中的每個字元作為葉子結點生成一棵編碼二叉樹,為了獲得傳送報文的最短長度,可將每個字元的出現頻率作為字元結點的權值賦予該結點上,顯然字使用頻率越小權值越小,權值越小葉子就越靠下,於是頻率小編碼長,頻率高編碼短,這樣就保證了此樹的最小帶權路徑長度效果上就是傳送報文的最短長度。因此,求傳送報文的最短長度問題轉化為求由字元集中的所有字元作為葉子結點,由字元出現頻率作為其權值所產生的哈夫曼樹的問題。利用哈夫曼樹來設計二進制的前綴編碼,既滿足前綴編碼的條件,又保證報文編碼總長最短。
哈夫曼靜態編碼:它對需要編碼的數據進行兩遍掃描:第一遍統計原數據中各字元出現的頻率,利用得到的頻率值創建哈夫曼樹,並必須把樹的信息保存起來,即把字元0-255(2^8=256)的頻率值以2-4BYTES的長度順序存儲起來,(用4Bytes的長度存儲頻率值,頻率值的表示範圍為0--2^32-1,這已足夠表示大檔案中字元出現的頻率了)以便解壓時創建同樣的哈夫曼樹進行解壓;第二遍則根據第一遍掃描得到的哈夫曼樹進行編碼,並把編碼後得到的碼字存儲起來。
哈夫曼動態編碼:動態哈夫曼編碼使用一棵動態變化的哈夫曼樹,對第t+1個字元的編碼是根據原始數據中前t個字元得到的哈夫曼樹來進行的,編碼和解碼使用相同的初始哈夫曼樹,每處理完一個字元,編碼和解碼使用相同的方法修改哈夫曼樹,所以沒有必要為解碼而保存哈夫曼樹的信息。編碼和解碼一個字元所需的時間與該字元的編碼長度成正比,所以動態哈夫曼編碼可實時進行。
2、哈夫曼解碼
在通信中,若將字元用哈夫曼編碼形式傳送出去,對方接收到編碼後,將編碼還原成字元的過程,稱為哈夫曼解碼。
基本術語
哈夫曼樹又稱為最優樹.
1、路徑和路徑長度
在一棵樹中,從一個結點往下可以達到的孩子或孫子結點之間的通路,稱為路徑。通路中分支的數目稱為路徑長度。若規定根結點的層數為1,則從根結點到第L層結點的路徑長度為L-1。
2、結點的權及帶權路徑長度
若將樹中結點賦給一個有著某種含義的數值,則這個數值稱為該結點的權。結點的帶權路徑長度為:從根結點到該結點之間的路徑長度與該結點的權的乘積。
3、樹的帶權路徑長度
樹的帶權路徑長度規定為所有葉子結點的帶權路徑長度之和,記為WPL。
構造
假設有n個權值,則構造出的哈夫曼樹有n個葉子結點。 n個權值分別設為 w1、w2、…、wn,則哈夫曼樹的構造規則為: 哈夫曼樹的構造
哈夫曼樹的構造
 哈夫曼樹的構造
哈夫曼樹的構造(1) 將w1、w2、…,wn看成是有n 棵樹的森林(每棵樹僅有一個結點);
(2) 在森林中選出兩個根結點的權值最小的樹合併,作為一棵新樹的左、右子樹,且新樹的根結點權值為其左、右子樹根結點權值之和;
(3)從森林中刪除選取的兩棵樹,並將新樹加入森林;
(4)重複(2)、(3)步,直到森林中只剩一棵樹為止,該樹即為所求得的哈夫曼樹。
多叉哈夫曼樹
哈夫曼樹也可以是k叉的,只是在構造k叉哈夫曼樹時需要先進行一些調整。構造哈夫曼樹的思想是每次選k個權重最小的元素來合成一個新的元素,該元素權重為k個元素權重之和。但是當k大於2時,按照這個步驟做下去可能到最後剩下的元素少於k個。解決這個問題的辦法是假設已經有了一棵哈夫曼樹(且為一棵滿k叉樹),則可以計算出其葉節點數目為(k-1)nk+1,式子中的nk表示子節點數目為k的節點數目。於是對給定的n個權值構造k叉哈夫曼樹時,可以先考慮增加一些權值為0的葉子節點,使得葉子節點總數為(k-1)nk+1這種形式,然後再按照哈夫曼樹的方法進行構造即可。
實現方法
數據壓縮
一開始,所有的節點都是終端節點,節點內有三個欄位:
1.符號(Symbol)
2.權重(Weight、Probabilities、Frequency)
3.指向父節點的連結(Link to its parent node)
而非終端節點內有四個欄位:
1.權重(Weight、Probabilities、Frequency)
2.指向兩個子節點的連結(Links to two child node)
3.指向父節點的連結(Link to its parent node)
基本上,我們用'0'與'1'分別代表指向左子節點與右子節點,最後為完成的二叉樹共有n個終端節點與n-1個非終端節點,去除了不必要的符號並產生最佳的編碼長度。
過程中,每個終端節點都包含著一個權重(Weight、Probabilities、Frequency),兩兩終端節點結合會產生一個新節點,新節點的權重是由兩個權重最小的終端節點權重之總和,並持續進行此過程直到只剩下一個節點為止。
實現哈夫曼樹的方式有很多種,可以使用優先佇列(Priority Queue)簡單達成這個過程,給與權重較低的符號較高的優先權(Priority),算法如下:
⒈把n個終端節點加入優先佇列,則n個節點都有一個優先權Pi,1 ≤ i ≤ n
⒉如果佇列內的節點數>1,則:
- ⑴從佇列中移除兩個最小的Pi節點,即連續做兩次remove(min(Pi), Priority_Queue)
- ⑵產生一個新節點,此節點為(1)之移除節點之父節點,而此節點的權重值為(1)兩節點之權重和
- ⑶把(2)產生之節點加入優先佇列中
⒊最後在優先佇列里的點為樹的根節點(root)
而此算法的時間複雜度(Time Complexity)為O(n log n);因為有n個終端節點,所以樹總共有2n-1個節點,使用優先佇列每個循環須O(log n)。
此外,有一個更快的方式使時間複雜度降至線性時間(Linear Time)O(n),就是使用兩個佇列(Queue)創件哈夫曼樹。第一個佇列用來存儲n個符號(即n個終端節點)的權重,第二個佇列用來存儲兩兩權重的合(即非終端節點)。此法可保證第二個佇列的前端(Front)權重永遠都是最小值,且方法如下:
⒈把n個終端節點加入第一個佇列(依照權重大小排列,最小在前端)
⒉如果佇列內的節點數>1,則:
- ⑴從佇列前端移除兩個最低權重的節點
- ⑵將(1)中移除的兩個節點權重相加合成一個新節點
- ⑶加入第二個佇列
⒊最後在第一個佇列的節點為根節點
雖然使用此方法比使用優先佇列的時間複雜度還低,但是注意此法的第1項,節點必須依照權重大小加入佇列中,如果節點加入順序不按大小,則需要經過排序,則至少花了O(n log n)的時間複雜度計算。
但是在不同的狀況考量下,時間複雜度並非是最重要的,如果我們考慮英文字母的出現頻率,變數n就是英文字母的26個字母,則使用哪一種算法時間複雜度都不會影響很大,因為n不是一筆龐大的數字。
數據解壓縮
簡單來說,哈夫曼碼樹的解壓縮就是將得到的前置碼(Prefix Huffman code)轉換回符號,通常藉由樹的追蹤(Traversal),將接收到的比特串(Bits stream)一步一步還原。但是要追蹤樹之前,必須要先重建哈夫曼樹;某些情況下,如果每個符號的權重可以被事先預測,那么哈夫曼樹就可以預先重建,並且存儲並重複使用,否則,傳送端必須預先傳送哈夫曼樹的相關信息給接收端。
最簡單的方式,就是預先統計各符號的權重並加入至壓縮之比特串,但是此法的運算量花費相當大,並不適合實際的套用。若是使用Canonical encoding,則可精準得知樹重建的數據量只占B2^B比特(其中B為每個符號的比特數(bits))。如果簡單將接收到的比特串一個比特一個比特的重建,例如:'0'表示父節點,'1'表示終端節點,若每次讀取到1時,下8個比特則會被解讀是終端節點(假設數據為8-bit字母),則哈夫曼樹則可被重建,以此方法,數據量的大小可能為2~320位元組不等。雖然還有很多方法可以重建哈夫曼樹,但因為壓縮的數據串包含"traling bits",所以還原時一定要考慮何時停止,不要還原到錯誤的值,如在數據壓縮時時加上每筆數據的長度等。
示例
- 當有100個位子,有白色占60%、咖啡色占20%,藍色和紅色各占10%,則該如何分配才能最最佳化此座位?
(a)direct:
假設結果為:白色為00、咖啡色01,藍色10和紅色11個bits則結果為:100*2 = 200bits
(b)huffman code: (must be satisfy the following conditions,if not change the node)
(1) 所有碼皆在Coding Tree的端點,再下去沒有分枝(滿足一致解碼跟瞬間解碼)
(2) 機率越大,code length越短;機率越小,code length越長
(3) 假設 是第L層的node,
是第L層的node,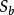 是第L+1層的node
是第L+1層的node
假設結果為:白色為00、咖啡色01,藍色10和紅色11個bits則結果為:100*2 = 200bits
(b)huffman code: (must be satisfy the following conditions,if not change the node)
(1) 所有碼皆在Coding Tree的端點,再下去沒有分枝(滿足一致解碼跟瞬間解碼)
(2) 機率越大,code length越短;機率越小,code length越長
(3) 假設

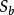
則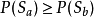 必須滿足
必須滿足
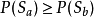
假設結果為:白色占0、咖啡色10,藍色110和紅色111個bits
則結果為:60*1+20*2+20*3=160bits
則結果為:60*1+20*2+20*3=160bits
相互比較兩個結果huffman code 整整少了40bits的存儲空間。