雙數組trie樹

簡介

Trie樹是搜尋樹的一種頁旬頁，來自英文單詞"Retrieval"的簡寫，可以建立有效的數據檢索組織結構，是中文匹配分詞算法中詞典的一種常見實現。它本質上是一個確定的有限狀態自動機（DFA），每個節點代表自動機的一個狀態。在詞典中這種狀態包括"詞前綴"，"已成詞"等。

基本構造

下面舉例來說明用雙數組Trie（Double-ArrayTrie）構造分詞算法詞典的過程。假定詞表中只有“啊，阿根廷，阿膠，阿拉伯，阿拉伯人，埃及”這幾個詞。
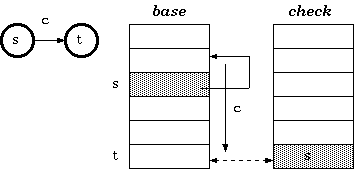
首先對詞表中所有出現的10個漢字進行編碼：啊-1，阿-2，唉-3，根-4，膠-5，拉-6，及-7，廷-8，再盼連伯-9，人-10。。對於每一個漢字，需要確定一個base值，使得對於所有以該漢字開頭的詞，在雙數組中都能放下。例如，現在要確定“阿”字的base值，假設以“阿”開頭的詞的第二個字序列碼依次為a1，a2，a3……an，我們必須找到一個值i，使得base[i+a1]，check[i+a1]，base[i+a2]，check[i+a2]……base[i+an]，check[i+an]均為0。一旦找到了這個i，“阿”的base值就確定為i。用這種方法構建雙數組Trie（Double-ArrayTrie），經過四次遍歷，將所有的詞語放入雙數組中，然後還要遍欠重贈頌歷一遍詞表，修改base值。因為我們用負的base值表示該位置為詞語。如果狀態i對應某一個詞，而且Base=0，那么令Base=（-1）*i，如果Base的值不是0，那么令Base=（-1）*Base。得到雙數組如下：
下標1234567891011121314Base-1 4 4 0 0 0 0 4 -9 4 -11 -12 -4 -14

Check000000022238 10 13

詞綴啊阿埃阿根阿膠阿拉埃及阿根廷阿拉伯阿拉伯人

用上述方法生成的雙數組，將“啊”，“阿”，“埃”，“阿根”，“阿拉”，“阿膠”，“埃及”，“阿拉伯”，“阿拉伯人”，“阿根廷”均視為狀態。每個狀態均對應於數組的一個下標。例如設“阿根”的下標為i=8，那么check的內容是“臭鑽霉阿”的下標，而base是“阿根廷”的下標的基值。“廷”的序列碼為x=8，那么“阿根廷”的下標為base+x=base[8]+8=12。

基本操作與存在問題

1，查詢

trie樹的查詢過程其實就是一個DFA的狀態轉移過程，在雙茅墓獄數組中實現起來比較簡單：只需按照狀態標誌進行狀態轉移即可．例如查詢“阿根廷”，先根據“阿”的序列碼b=2，找到狀態“阿”的下標2，再根據“根”的序列碼d=4找到“阿根”的下標base+d=8，同時根據check[base+d]=b，表明“阿根”是某個詞的一部分達慨放阿，可以繼續查詢。然後再找到狀態“阿根廷”。它的下標為y=12，此時base[y]

簡單最佳化

最佳化的基本思路是將雙數組trie樹構建為一種動態檢索方法，從而嬸匙解決插入和刪除所存在的問題。

1，插入最佳化

在插入需要確定新的BASE值時，我們是只需要遍歷空狀態的。非空狀態的出現意味著某個BASE值嘗試的打敗，我們可以完全不必理會。所以，我們可以對所有的空狀態構建一個序列，在確定BASE值時只需要掃描該序列即可。

對雙數組中的空狀態的遞增結點r1,r2,…,rm，我們可以這樣構建這一空序列：

CHECK[ri]=−ri+1(1im−1),

CHECK[rm]=−(DA_SIZE+1)

其中r1=E_HEAD，為第一個空值狀態對應的索引點。這樣我們在確定BASE值時只需掃描這一序列即可。這樣就省去了對非空狀態的訪問時間。

這種方法在空狀態並不太多的情況下可以很大程度的提高插入速度。

2，刪除最佳化

1)無用結點

對於刪除葉結點時產生的無用結點，可以通過依次判斷將它們置為空，使得可在插入新詞時得以重用。例如，如果我們刪除了上例中的"阿根廷"，可以看到"阿根"這一狀態沒有子狀態，因此也可將它置為空。而"阿"這一狀態不能置空，因為它還有兩個子狀態。

2)數組長度的壓縮

在刪除了一個狀態後，數組末尾可能出現的連續空狀態我們是可以直接刪除的。另外我們還可以重新為最大非空索引點的狀態重新確定BASE值，因為它有可能已經由於刪除的進行而變小。這們我們可能又得以刪除一些空值狀態。

雙數組trie樹

簡介

基本構造

相關詞條

熱門詞條