雙三次插值

雙三次插值，英文是Bicubic interpolation。

雙三次插值是一種更加複雜的插值方式，它能創造出比雙線性插值更平滑的圖像邊緣。雙三次插值方法通常運用在一部分圖像處理軟體、印表機驅動程式和數位相機中，對原圖像或原圖像的某些區域進行放大。Adobe Photoshop CS 更為用戶提供了兩種不同的雙三次插值方法：雙三次插值平滑化和雙三次插值銳化。

基本介紹

• 中文名：雙三次插值
• 外文名：Bicubic interpolation
• 定義：是一種更加複雜的插值方式
• 屬性：一階偏導數和交叉導數處處連續
• 相關術語：雙線性插值
• 套用學科：數學

定義

在數值分析這個數學分支中，雙三次插值（英語：Bicubic interpolation）是二維空間中最常用的插值方法。在這種方法中，函式f在點 (x,y) 的值可以通過矩形格線中最近的十六個採樣點的加權平均得到，在這裡需要使用兩個多項式插值三次函式，每個方向使用一個。

雙三次插值又叫雙立方插值，用於在圖像中“插值”（Interpolating）或增加“像素”（Pixel）數量/密度的一種方法。通常利用插值技術增加圖形數據，以便在它列印或其他形式輸出的時候，能夠增大列印面積以及（或者）解析度。

目前有不同的插值技術可供選用。雙立方插值通常能產生效果最好，最精確的插補圖形，但它速度也幾乎是最慢的。“雙線性插值”（Bilinear interpolation）的速度則要快一些，但沒有前者精確。在商業性圖像編輯軟體中，經常採用的是速度最快，但也是最不準確的“最近相鄰”（Nearest Neighbor）插值。其他一些插值技術通常只在高檔或單獨套用的程式中出現。

顯然，無論技術多么高級，插補過的數據肯定沒有原始數據準確。這意味著對一個圖形檔案進行插值處理後，雖然檔案長度增加了（數據量增大），但不會有原先那幅圖銳利，可能會在圖形質量上打折扣。

屬性

通過雙三次插值可以得到一個連續的插值函式，它的一階偏導數連續，並且交叉導數處處連續。

公式

雙三次插值通過下式進行計算：

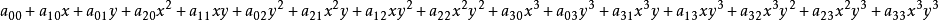
或者用一種更加緊湊的形式，

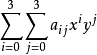
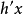計算係數的過程依賴於插值數據的特性。如果已知插值函式的導數，常用的方法就是使用四個頂點的高度以及每個頂點的三個導數。一階導數與 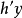表示 x 與 y 方向的表面斜率，二階相互導數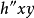表示同時在 x 與 y 方向的斜率。這些值可以通過分別連續對 x 與 y 向量取微分得到。對於格線單元的每個頂點，將局部坐標（0,0, 1,0, 0,1 和 1,1) 帶入這些方程，再解這 16 個方程。

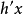
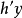
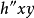
套用

雙三次插值算法經常用於圖像或者視頻的縮放，它能比占主導地位的雙線性濾波算法保留更好的細節質量。