阿波羅尼奧斯軌跡定理是一個著名軌跡問題。若一動點至兩定點的距離之比等於兩不等的已知線段之比,則該點的軌跡是一個圓。
基本介紹
- 中文名:阿波羅尼奧斯軌跡定理
- 外文名:Apollonius locus theorem
- 適用範圍:數理科學
- 提出學者:古希臘數學家阿波羅尼奧斯
定理簡介,問題簡介,
定理簡介
阿波羅尼奧斯軌跡定理是一個著名軌跡問題。
若一動點至兩定點的距離之比等於兩不等的已知線段之比,則該點的軌跡是一個圓。如果 A,B 為定點,P 是動點,a,b 為不等的已知線段,PA/PB=a/b,Q,R 為線段 AB 的內、外分點,即 QA/QB=RA/RB=a/b,則點的軌跡是以 QR 為直徑的圓(如圖)。
這個圓稱為阿波羅尼奧斯圓。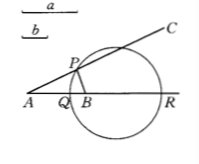 圖1.
圖1.
 圖1.
圖1.問題簡介
阿波羅尼奧斯問題是由公元前 3 世紀下半葉古希臘數學家阿波羅尼奧斯提出的幾何作圖問題,載於他的《論接觸》中,惜原書已失傳。後來公元 4 世紀學者帕波斯記載了其中所提出的一個作圖問題:設有 3 個圖形,可以是點、直線或圓,求作一圓通過所給的點(如果3個圖形中包含點的話)並與所給直線或圓相切。當中共有 10 種可能情形,其中最著名的是:求作一圓與3個已知圓相切,常稱為阿波羅尼奧斯問題( Apollonius'problem)。據說阿波羅尼奧斯本人解決了問題,可惜結果沒有流傳下來。
1600年法國數學家韋達在一篇論著中套用了兩個圓相似中心的歐幾里得解法,通過對每一種特殊情況的討論,嚴格陳述了該問題的解。後來牛頓、蒙日、高斯等許多數學家都對這一問題進行過研究,得到多種解決方法。 其中以法國數學家熱爾崗約於1813年給出的解法較有代表性。以上所說都是通常的標尺作圖法。如果放寬作圖條件限制,則有多種簡捷的解法。
