閘壩非岩石地基中恆定滲流的一種近似計算方法。可用以確定滲流區中各處的滲流要素, 包括滲透壓力、滲透坡降和滲透流量。這一方法是丘加也夫(Р.Р.Чугаев)根據巴甫洛夫斯基分段法的理論和努麥羅夫對急變滲流區計算的理論在1957年提出的。
阻力係數法計算簡便,精度較高,一般誤差不超過5%,為工程設計計算所採用。但是,這一方法尚存在著不能計算板樁尖點水頭等問題。中國學者對阻力係數法作了改進,增加了用通過板樁尖點的等勢線劃分滲流區,再用努麥羅夫對急變滲流區求得的解析解計算各分段的阻力係數。
基本介紹
- 中文名:阻力係數法
- 外文名:method of resistance coefficient
套用阻力係數法計算時,首先需要將建築物底面下的整個滲透區劃,分成幾個流段。丘氏用通過地下輪廓各轉折點(板樁尖點除外)的等勢線分段,並將各流段歸納為3種基本類型:①進口段或出口段,如圖1中的Ⅰ、Ⅴ段;②中間板樁段或中間齒坎段,如圖1中的Ⅲ段;③水平段,如圖1中的Ⅱ、Ⅳ段。
滲流經過任一段的水頭損失hi可相應計算得到。q為單寬滲流量;K為地基土的滲透係數;ζi為阻力係數,是該流段的滲流特徵值,只與滲透區的幾何形狀有關,為邊界條件的函式,可以用流體力學的精確解求得。
整個滲透區的總水頭損失H等於各流段水頭損失之和。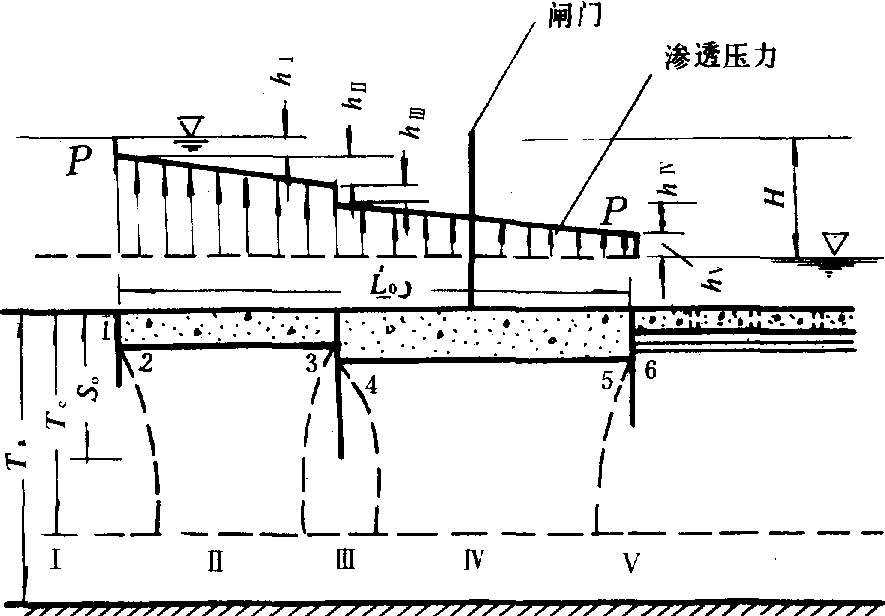

阻力係數法的分段及基底滲透壓力分布
由於整個滲透區總的水頭損失H為一定值,任一流段水頭損失的大小與該段的阻力係數成正比。因此,在進行地下輪廓布置時,可用比較不同流段ζi值大小的辦法來分析地下輪廓各部分的相對滯滲效果。
求出各段水頭損失值後,由出口處向上游疊加,得到各分界面處水頭,兩分界面間的水頭損失近似認為按直線變化,於是可以繪出基底的滲透水頭線P-P(圖1),從而可求出作用於閘壩底面上的滲透壓力。但當出口板樁較短或無板樁時,由上述計算得到的出口段水頭損失值誤差較大,需要對出口附近的壓力水頭線作局部修正(圖2)。修正的方法是:設未經修正的出口段水頭損失為h0,將其乘以修正係數ζ,即得修正後的出口段水頭損失h′0。
當0.7≤T2/T1≤1.0時,ζ值可計算出。式中S為板樁長度;T1、T2為板樁兩側地基透水層深度。取修正範圍為0.1L0(L0為地下輪廓線水平投影長度),並在壓力水頭線上找出與0.1L0及h′0相對應的M、N′兩點,以直線連線這兩點,所得的MN′P線即為修正後的出口附近壓力水頭線。

出口壓力局部修正圖
阻力係數法適用於地基不透水層埋藏較淺的情況,當不透水層埋藏很深或無限深時,在進行上述計算之前,先要確定一個計算深度Tc,並用Tc去代替實際深度Ta(圖1)。L0為地下輪廓線的水平投影長度;S0為地下輪廓線的鉛直投影長度;A,B為係數。當L0/S0≥5時,A=0,B=0.5;當L0/S0=5~3.4時,A=2.5,B=0;當L0/S0=3.4~1.0時,A=0.8,B=0.5;當L0/S0=1.0~0時,A=1.0,B=0.3。
下游出口處滲流的出逸比降Je,可按努麥羅夫的近似公式進行計算。H為滲透區的總水頭損失;ζi為阻力係數;a為係數。T′c為計算出逸比降所採用的計算深度,T′c=2Tc。當實際透水層深度Ta>T′c時,計算深度取用T′c;如實際透水層深度Ta<T′c,計算深度取用Ta。
阻力係數法計算簡便,精度較高,一般誤差不超過5%,為工程設計計算所採用。但是,這一方法尚存在著不能計算板樁尖點水頭等問題。中國學者對阻力係數法作了改進,增加了用通過板樁尖點的等勢線劃分滲流區,再用努麥羅夫對急變滲流區求得的解析解計算各分段的阻力係數。由於改進阻力係數法能求得板樁尖點的水頭,可以直接求出實用上的出逸比降;加之補充了傾斜底板和齒牆不規則部分等的計算方法,既擴大了計算範圍,又提高了計算精度,因而該改進法已在實際工程的設計計算中得到套用。
