鑲嵌摺紙

鑲嵌摺紙（Origami Tessellations），指通過紙張摺疊形成的立體結構來實現密鋪；最初由日本數學家藤本修三（Shuzo Fujimoto）於1970年代創作；它是國際摺紙奧林匹克競賽（International Origami Internet Olympiad）的必考賽題，是摺紙奧運項目之一。

基本介紹

• 中文名：鑲嵌摺紙 
• 外文名：Origami Tessellations 
• 別名：密鋪摺紙 
• 相關比賽：國際摺紙奧林匹克 
• 所屬項目：摺紙奧運項目 

鑲嵌

鑲嵌（Tessellation，又譯為“密鋪”）是了解鑲嵌摺紙的前提；它指全等形能不重疊、無間隙地鋪滿平面；如：埃舍爾的視錯覺畫作、街頭巷尾的磚鋪路面。

埃舍爾的視錯覺畫作

而鑲嵌摺紙則憑藉紙張摺疊形成的立體結構來實現這一點，且僅使用一張紙，不經剪裁或膠粘；部分鑲嵌摺紙不僅正反兩面均為極富觀賞性的鑲嵌圖形，還能任意且順暢地展開復原。

扭轉

扭轉（Twist）是鑲嵌摺紙的基礎。

扭轉的關鍵，從圖1的摺痕中很容易發現——以一個凸多邊形為中心，自其每一邊“發出”兩條摺疊方向相異的平行線。這組平行線與邊所成的角度並不是固定的，圖2中可以觀察到角度對紙張重疊面積的影響。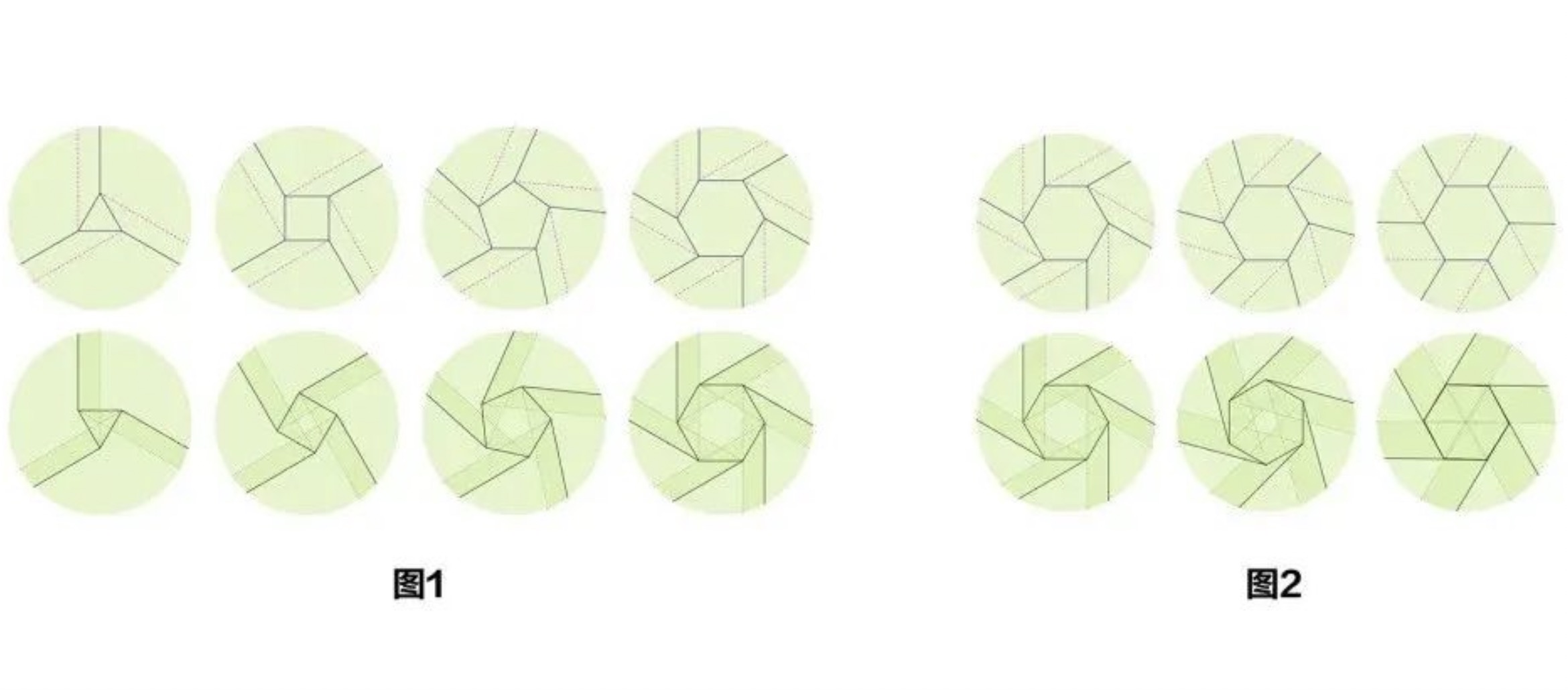

圖1、圖2

除了摺疊面積，這一角度也決定了扭轉的方向（圖3），以及扭轉前後中心多邊形轉過的角度——後者是前者的兩倍（圖4）。事實上，中心凸多邊形甚至不必是正多邊形，只不過其中所牽涉的幾何學計算不那么優雅罷了。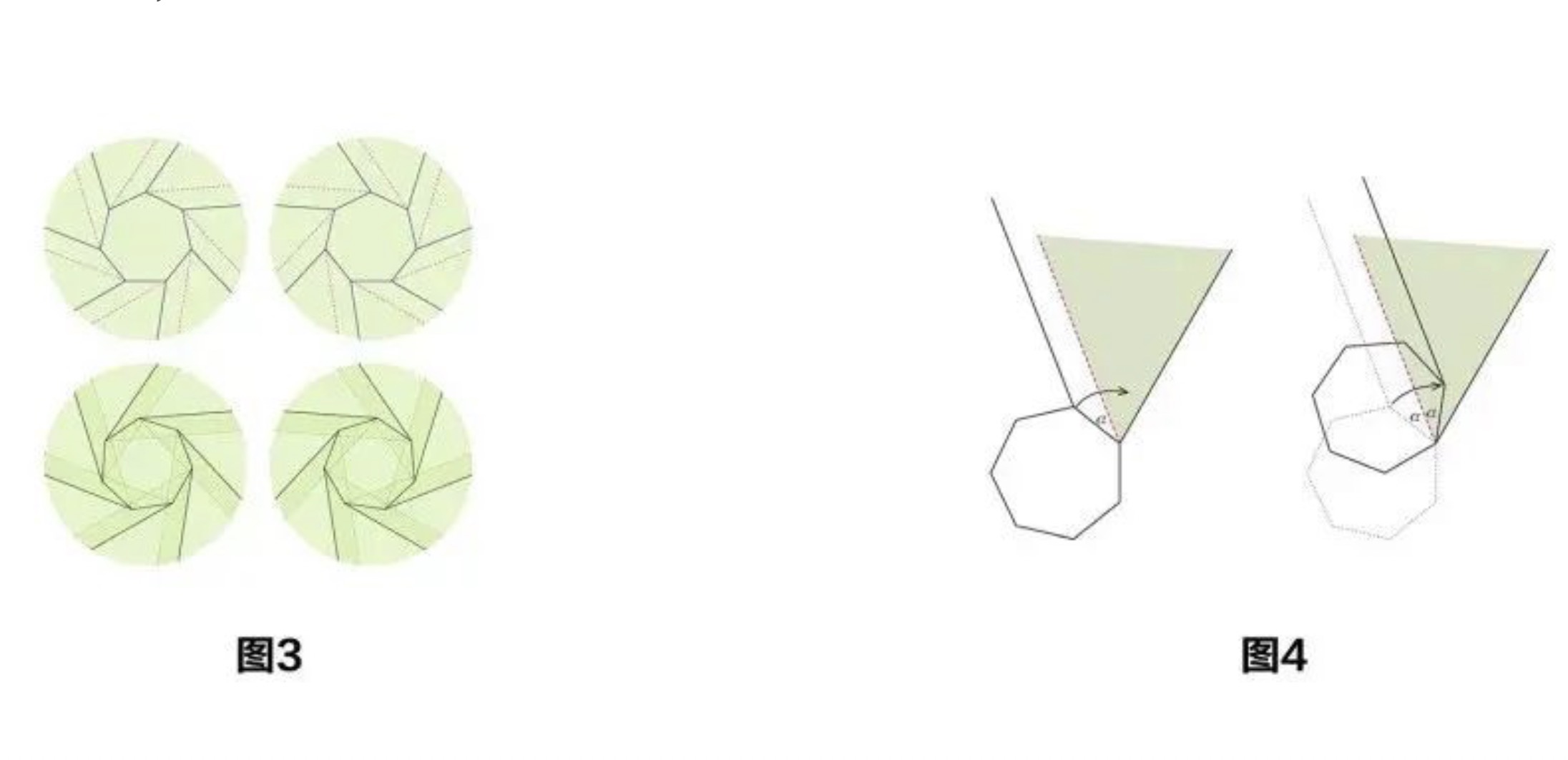

圖3、圖4

單單是作為基礎的扭轉似乎已經花樣不少；而當扭轉被鑲嵌理論組合起來，通向無窮可能性的大門豁然洞開。將扭轉用其中心多邊形的相似形框起來，它便成為了一隻“晶胞”，可以在平面上無限地拼接（圖5、6）。雖說是“晶胞”，但其實這些小單元並不完全相同，其內部亦存在著周期性的“手性”變化——以保證摺痕的連續。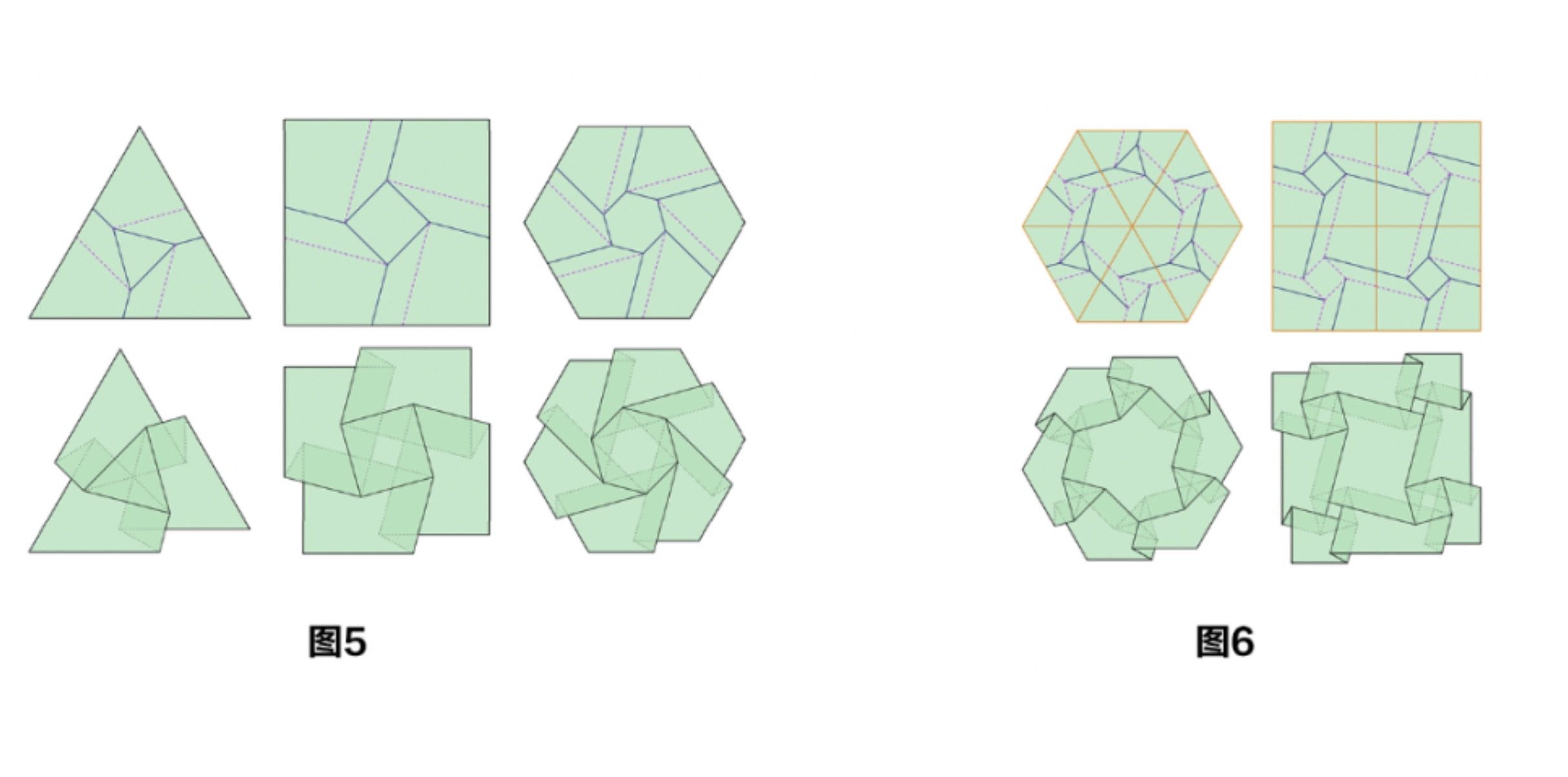

圖5、圖6

剝去扭轉的細節，僅觀察這些人為添加的橙色邊界，百年前徘徊於伊斯蘭建築的幾何學“幽靈”——鑲嵌問題——再次浮現於摺紙藝術（圖7）。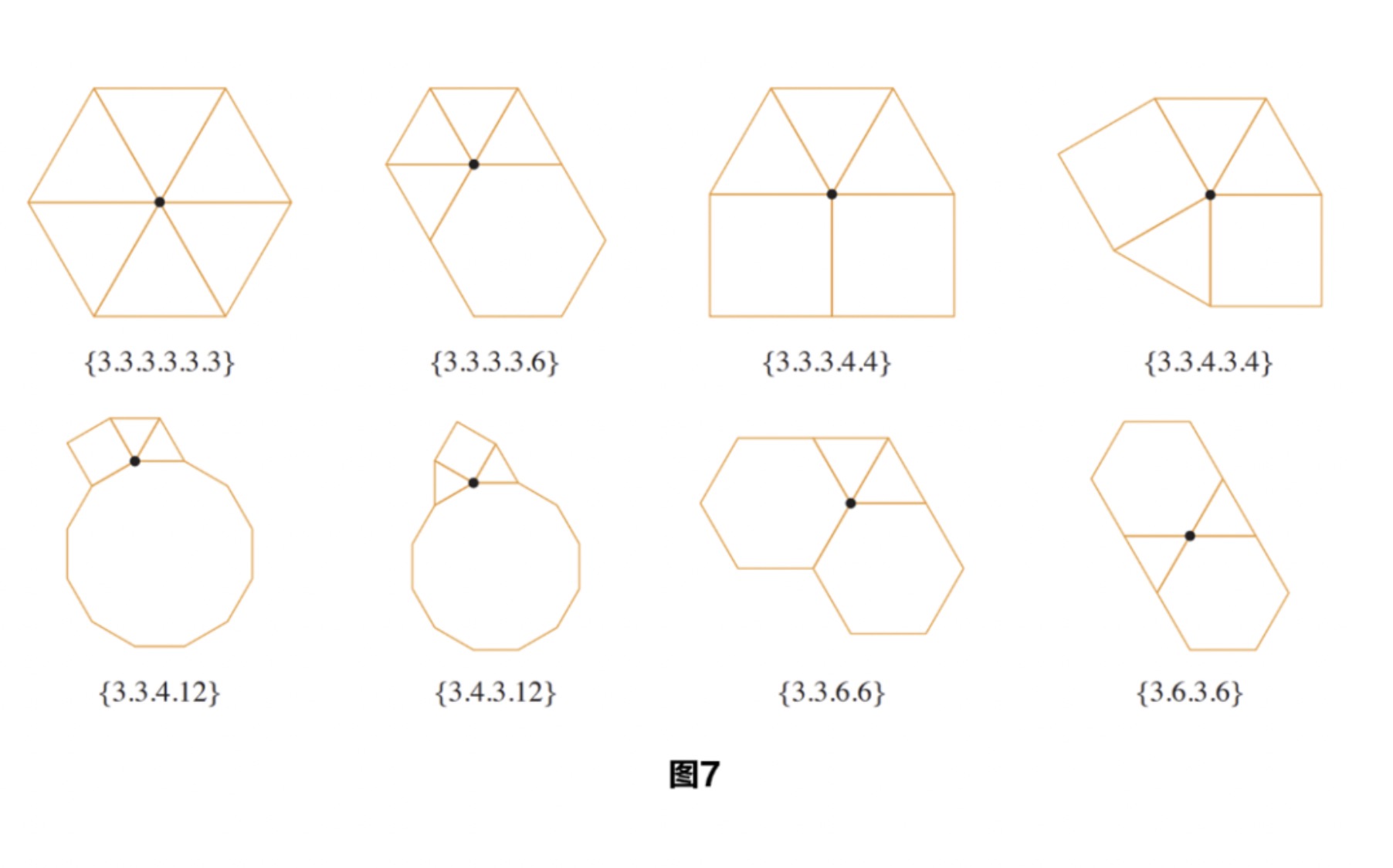

圖7

簡單的正多邊形經過一番似也不如何複雜的鑲嵌，其扭轉而成的鑲嵌摺紙卻令人眼花繚亂，理想幾何形抽象而迷人的韻律盤桓其間（圖8、圖9）。

圖8、圖9

套用

鑲嵌摺紙不僅是藝術和幾何學的具象，還能套用於工程領域，例如：

長投射式望遠鏡

2015年，羅伯特·朗作為加州勞倫斯利弗莫爾國家實驗室的長投射式望遠鏡的設計顧問，將“傘”式摺紙結構套用於該望遠鏡大而薄的光學鏡片（其主透鏡直徑達100米）。這一摺紙結構呈鏡像對稱，可保持穩定自旋；其摺疊狀態適於在火箭運輸；它也可擴展；其部件可大規模生產。

太陽能電池板

日本衛星曾搭載基於摺紙的摺疊式太陽能電池板。

新型心臟支架

一種新型心臟支架受啟發自紙折球。

安全氣囊

安全氣囊展開算法來自於研究紙折昆蟲的數學理論。

評價

摺紙仍然在蓬勃地發展著，鑲嵌摺紙亦方興未艾；科學與藝術必仍在這一方紙上交輝。（新浪科技評）