如果一個關鍵字可以表示成字元的序號,即字元串,那么可以用鍵樹(keyword tree),又稱數字搜尋樹(digital search tree)或字元樹,來表示這樣的字元串的集合。
基本介紹
- 中文名:鍵樹
- 外文名:keyword tree
- 又稱:數字搜尋樹
- 作用:數字串中一數位,單詞中一字母
概念,鍵樹的存儲,代碼實現,
概念
如果一個關鍵字可以表示成字元的序號,即字元串,那么可以用鍵樹(keyword tree),又稱數字搜尋樹(digital search tree)或字元樹,來表示這樣的字元串的集合。鍵樹又稱為數字查找樹(Digital Search Tree)或Trie樹(trie為retrieve中間4個字元),其結構受啟發於一部大型字典的“書邊標目”。字典中標出首字母是 A,B,C,....Z的單詞所在頁,再對各部分標出第二字母為A,B,C,...Z的單詞所在的頁, ....等等。
鍵樹是一種特殊的查找樹,它的某個節點不是包含一個或多個關鍵字,而是只包含組成關鍵字的一部分(字元或數字),比如:如果關鍵字是數值,則節點中只包含一個數位;如果關鍵字是單詞,則節點中只包含一個字母字元。
根結點不代表任何字元,根以下第一層的結點對應於字元串的第一個字元,第二層的結點對應於字元串的第二個字元……每個字元串可由一個特殊的字元如“$”等作為字元串的結束符,用一個葉子結點來表示該特殊字元。把從根到葉子的路徑上,所有結點(除根以外)對應的字元連線起來,就得到一個字元串。因此,每個葉子結點對應一個關鍵字。在葉子結點還可以包含一個指針,指向該關鍵字所對應的元素。整個字元串集合中的字元串的數目等於葉子結點的數目。如果一個集合中的關鍵字都具有這樣的字元串特性,那么,該關鍵字集合就可採用這樣一棵鍵樹來表示。事實上,還可以賦予“字元串”更廣泛的含義,它可以是任何類型的對象組成的串。常見鍵樹如圖所示: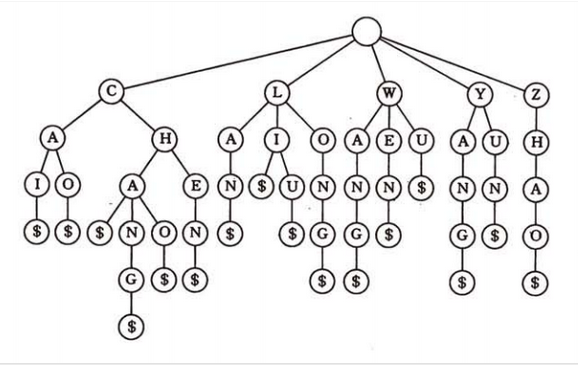

鍵樹的存儲
鍵樹的存儲通常有兩種方式:
(1)雙鏈樹表示
如果以樹的孩子兄弟表示,則每個節點包含3個域。
A: symbol域: 存儲關鍵字的一個字元 ;B: son域: 存儲指向第一棵子樹的根的指針。葉子節點的son域指向該關鍵字記錄的指針 ;C: brother域: 存儲指向右兄弟的指針。這時的鍵樹又稱為雙鏈樹。關鍵代碼如下:
//雙鏈樹的存儲表示
typedef struct DULNode{
char symbol; //結點字元域
struct DULNode *son, *brother; //son指向子樹根結點,brother指向右兄弟結點.
}DULNode ,*DLTree;
(2) 多重鍊表表示
如果以樹的多重鍊表表示鍵樹, 則樹的每個結點中應包含d個(d為關鍵字元的基,如:字元集由英文大寫字母構成時,則d=26+1=27)指針域,此時的鍵樹又稱為Trie樹。Trie樹中有兩種結點:
(1)分支結點:含有d個指針域,整數n記錄非空指針域的個數(可選)。
(2)葉子結點:含有關鍵字域(完整的關鍵字、可選)、附加數據域名(可選)。
實際實現的時候,一般都只包含那d個指針域。在標準Trie樹的基礎上,可以壓縮:若從鍵樹中某個結點到葉子結點的路徑上每個結點都只有一個孩子,則可將該路徑上的所有結點壓縮成一個葉子結點。
代碼實現
一個標準Trie樹的Java實現如下:
import java.util.Arrays;
public class TrieNode {
public TrieNode() {
ptr = new TrieNode[BRANCH];
Arrays.fill(ptr, null);
}
public static final int BRANCH = 27;
public TrieNode[] ptr = null;
public int nptr = 0;
}
public class Trie {
public Trie() {
root = new TrieNode();
}
public void Insert(String key) {
TrieNode p = root;
for (int i = 0; i < key.length(); i++) {
int offset = key.charAt(i) - 'a';
if (p.ptr[offset] == null) {
p.ptr[offset] = new TrieNode();
p.nptr++;
}
p = p.ptr[offset];
}
}
public boolean Search(String key) {
TrieNode p = root;
for (int i = 0; i < key.length(); i++) {
int offset = key.charAt(i) - 'a';
if (p.ptr[offset] == null) {
return false;
}
p = p.ptr[offset];
}
return true;
}
private TrieNode root = null;
public static void main(String[] args) {
Trie trie = new Trie();
trie.Insert("liheyuan");
trie.Insert("liheyuan");
System.out.println(trie.Search("liheyuan"));
}
}
