基本介紹
- 中文名:配分比例
- 外文名:distributive proportion
- 所屬學科:數學
- 所屬問題:算術(比及比例)
- 簡介:把已知量按給定的比分為若干份
基本介紹,配分比例的意義,相關概念,解題方法與例題解析,
基本介紹
配分比例的意義
按—定的連比,將一數量分作若干分,叫做配分比例。其方法分為兩種,一用單比例求法,一用分數求法。單比例的求法:以連比相加為共比作第一項,被分的全量作第三項,把連比的各項各作第二項,所求的各分就是第四項。
配分比例的解法:
(一)將連比相加得共比。
(二)求各分所占全量之分數。
(三)用各分所占之分數乘全量,就得所求之各分。
注意:二種解法,以第二種方法為最便。
相關概念
連比的概念 單比表示任意兩個數量的比,複比表示若干個單比的前項乘積和後項乘積的比,至於連比,則是兩個以上數量的順次相比。例如:甲數是1,乙數是2,丙數是3,則甲、乙、丙三數的連比是1:2:3。
連比例的性質
(1)套用任何數乘(或除)連比的每一項,連比例式恆等
例如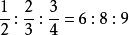 ,
,
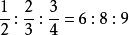
變換以後 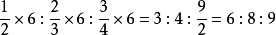 。
。
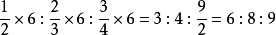
(2)連比例中,前比的各項互換,後比的各項作對應的互換,比例式恆等。
例如 1:3:5=2:6:10
變換以後 5:1:3=10:2:6
(3)連比例中,前比各項的和或差比各個項等於對應的後比各項的和或差比各個項。
例如 1:2:3=3:6:9
變換以後 1:2:3:1+2:2+3:1+2+3
=3:6:9:3+6:6+9:3+6+9
1:2:3:3:5:6=3:6:9:9:15:18。
解題方法與例題解析
1.單比例的求法 以連比相加為共比作第一項,被分的全量作第三項,把連比的各項各作第二項,所求的各分就是第四項。
【例1】以人民幣60元分給甲乙丙三個工人,使三人所得的比為3:2:1,求三人各分得幾元?
解1: 3+2+1=6為定比的和叫共比,作第一項。
6:3=60:X
∴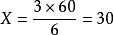 (甲)
(甲)
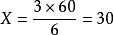
6:2=60:X
∴ (乙)
(乙)

6:1=60:X
∴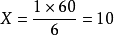 (丙)
(丙)
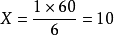
答:甲得20元,乙得20元,丙得10元。
2.配分比例的解法:
(一)將連比相加得共比。
(二)求各分所占全量之分數。
(三)用各分所占之分數乘全量,就得所求之各分。
注意:二種解法,以第二種方法為最便。
解2: 3+2+1=6 共比(即全分) -
甲占全數的 ;
;

乙占全數的 ;
;

丙占全數的 ,
,

∴甲得的元數為60元× =30元,
=30元,

乙得的元數為60元× =20元,
=20元,

丙得的元數為60元× =10元。
=10元。

【例2】將66分為甲乙丙三數,已知甲乙之比為3:2,乙丙之比為5:4,求三數各多少?
解:

甲數占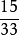 ,甲數為66×
,甲數為66×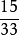 =30,
=30,
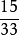
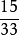
乙數占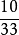 ,乙數為66×
,乙數為66×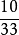 =20,
=20,
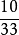
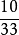
丙數占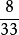 ,丙數為66×
,丙數為66×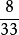 =16。
=16。