逼近問題(approximation problem)巴拿赫空間理論中的一個重要問題.設X是巴拿赫空間,若對X的每個緊子集K及每個:}0,都存在有限秩線性運算元T:X->X(即
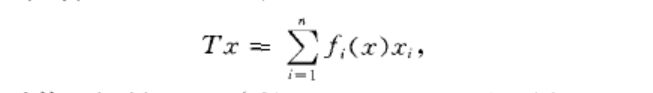
對某組{x;}',`-,CX,{f;}}`_,CX",bxEX),對每個xEK,均有日Tx-x }} }e,則稱巴拿赫空間X具有逼近性質.是否每個可分巴拿赫空間都有逼近性質,這就是所謂逼近問題.若巴拿赫空間X有紹德爾基,則X必有逼近性質.因此,若基問題的回答是肯定的,則逼近問題的回答也是肯定的;若逼近問題是否定的,則基問題也是否定的。恩夫洛(Enf1o,P.)找到了一個可分自反巴拿赫空間不具有逼近性質,從而既解決了逼近問題,也解決了基問題.
