連體力學

連續的概念源於數學。將連續的概念推理到物質上，可以說物質在空間裡是連續分布的。所謂連續物質從數學的觀點來看，其質量、動量與能量密度皆存在的物質。因此研究這種物質的力學，被稱為連續力學。

基本介紹

• 中文名：連續力學
• 外文名：continum mechanics
• 運用領域：物理學等
• 研究對象：連續物質

概念

力學是研究物質運動及其引起連動的力的科學。而連續力學是研究連續物質的力學。連續之一概念來自於數學。所謂連續物質是從數學角度來看其質量、動量與能量密度皆存在的物質。

研究內容

1. 向量及張量
2. 應力
3. 主應力與應力主軸
4. 形變分析
5. 速度場與相容性條件
6. 本構方程
7. 等向性
8. 流體與固體的力學性質
9. 場方程的演變
10. 流體的場方程式與邊界條件
11. 彈性問題

連續物質的理解

在數學觀念中，實數系是個連續的系統，即任意兩個相鄰的實數之間，必有另外一個實數。由此推知，任意兩個實數之間有無數多個實數。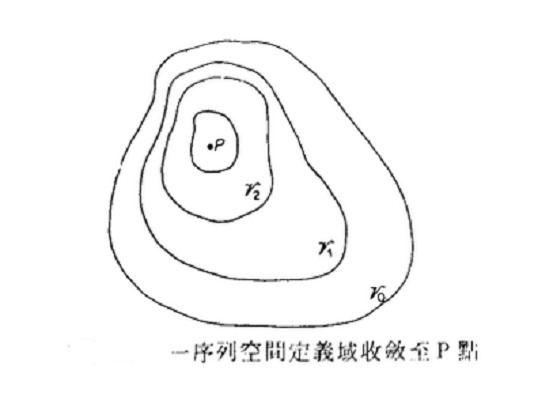

圖1

將連續的觀念推理到物質之上，可以說物質在空間上式連續分布的。這最好拿密度的觀念來解釋。假設物質的總量用質量來表示，且一些物質分布在某一空間 ，如圖1所示，考慮到 中的一點 ，同時一系列的部分空間 、 、 ……收斂至 。

設 的體積為 ，包含於 中物質的質量為 。當 且 時，求出 的比值；加假如 極限存在， 此極限值被認定為 點物質處的密度。表示為：

若密度在 中到處完全被定義著，則物質為連續分布的。

同理，可以定義動量、能量等密度。研究連續物質的力學，就被稱為連續力學。

連動定律與自由體系

連動力學，是建立在牛頓運動力學的基礎上，設坐標系統x₁，x₂，x₃為慣性坐標系，任何時間物體所在的空間用B_(r)表示，且r為質點與坐標系統原點相對位置的向量，ρ為物質密度，位在點(x₁,x₂,x₃)質點的體積為dv，質量為ρdv，速度向量為V。質點的線性動量為(ρdv)V對整個定域的積分，稱為形狀B_(r)內物體的線性動量，即：

再設對原點的動量矩為，故其對整個定義域的積分，稱為物體的動量矩：

最小位能原理

所有滿足內部一致性與邊界條件的方程，同時可滿足平衡方程使在穩定系中的位能最小。最小位能原理可由連體力學推得。此原理暗含一下條款：

每個物件皆可寫出位移方程。方程使一致的，同時確保節點相連的所有物件旋轉角度相同，並具有連續一階導數。

合併邊界條件使位移方程能滿足實際支撐情況。

將結構系的位移方程式用若干未知量表示。

在未定位移方程中，對未知位移作位能最小變化。

此四個方程式可以用來解，連線處的位移。一旦位移求出，則內力及每個構件的力矩也就可以求出。