辛普森多樣性指數

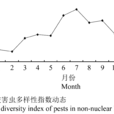
辛普森多樣性指數(Simpsonindex)該指數描述從一個群落種連續兩次抽樣所得到的個體數屬於同一種的機率。

基本介紹

• 中文名：辛普森多樣性指數
• 外文名：Simpson's diversity index
• 作用：判斷群落物種多樣性
• 公式：D=1−∑（Ni/N）^2
• 提出者：辛普森
• 別稱：優勢度指數

概念

辛普森多樣性指數是基於在一個無限大的群落中，隨機抽取兩個個體，它們屬於同一物種的機率是多少這樣的假設而推導出來的。

公式提出

辛普森在1949年提出過這樣的問題：在無限大小的群落中，隨機取樣得到同樣的個體標本，它們的機率是什麼呢？如果在加拿大北部寒帶森林中，隨機選取兩株樹，屬同一種的機率就很高。相反，如果在熱帶雨林隨機取樣，兩株樹同一種的機率很低，他從這個想法出發得出多樣性指數。

計算公式

辛普森多樣性指數=隨機取樣的兩個個體屬於不同種的機率=1-隨機取樣的兩個個體屬於同種的機率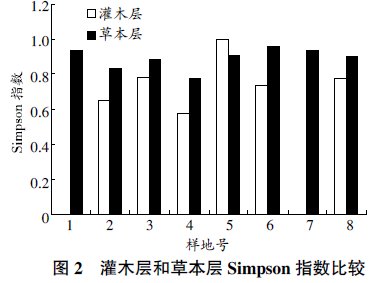

灌木和草本的辛普森指數

設種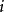 的個體數占群落中總個體數的比例為 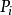,那么，隨機取種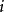兩個個體的聯合機率就為 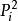。如果我們將群落中全部種的機率合起來，就可到辛普森指數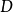，即

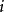
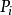
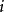
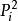
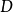
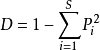
式中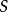，為物種數目。辛普森多樣性指數的最低值是0，最高值是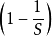。前一種情況出全部個體均屬於一個種的時候，後一種情況在每個個體分別屬於不同種的時候。

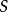
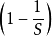
例題

甲群落中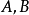兩種的個體數分別為 99 和 1 ，而乙群落中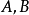兩種的個體數均為50，按辛普森多樣性指數計算，則甲、乙兩群落的多樣性指數分別為：

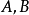
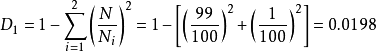
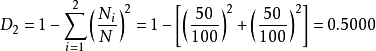
計算結果顯示：乙群落的多樣性高於甲群落。造成這兩個群落多樣性差異的主要原因是種的不均勻性，從豐富度看，兩個群落是一樣的，但從均勻度來看，二者是不同的。