基本介紹
簡介,定義公式,軸矢量的經典物理解釋,軸矢量的粒子物理解釋,極矢量和軸矢量的判別,刀軸矢量的控制方式,
簡介
軸矢量是指在鏡面對稱變換下法分量不變而切分量改變的矢量(宇稱為正的矢量),它是相對於極矢量而言的概念。矢量作為有方向的量,在坐標轉動時,分量隨坐標作相應變化。極矢量在宇稱變換(空間完全反演)下,大小不變,方向變得相反。軸矢量在宇稱變換下方向不改變。最常見的軸矢量,是角速度、角動量和磁感應強度。
定義公式
設有一矢量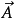 在關於平面
在關於平面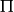 的鏡面反射變換
的鏡面反射變換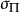 下滿足
下滿足
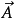
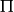
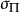

則稱矢量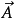 為軸矢量。
為軸矢量。
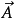
( 與
與  分別是
分別是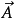 關於平面
關於平面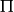 平行和垂直的分量)
平行和垂直的分量)


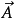
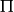
軸矢量的經典物理解釋
矢量作為有方向的量,在坐標轉動時,分量隨坐標作相應變化。極矢量在宇稱變換(空間完全反演)下,大小不變,方向變得相反。軸矢量在宇稱變換下方向不改變。最常見的軸矢量,是角速度、角動量和磁感應強度。它們與極矢量不同的一個明顯例子如下:一般而言,一個垂直鏡子的物體,在鏡子裡的像方向與自己相反;而一個轉軸與鏡子垂直的螺旋,在鏡子裡的像的旋轉方向跟實物的旋轉方向一樣,標誌其旋轉方向的矢量(角速度)也與實物的角速度方向相同。
一般而言,兩個極矢量的外積是軸矢量。
軸矢量的粒子物理解釋
在粒子物理里,既有矢量性質的流,又有軸矢量性質的流。特別重要的一個例子是弱相互作用相關的流,正好是矢量流和軸矢流之和。這樣的流由於既含有宇稱為正的部分又含有宇稱為負的部分,因此總的宇稱是不守恆的。這正是在弱相互作用下宇稱不守恆的根源。雖然流守恆的特性上,軸矢量流和矢量流並沒有什麼不一樣,但是在自然界中,矢量流是更為根本的。不僅除弱相互作用外的其他相互作用都是與矢量流相關的,而且在量子的層面上,軸矢流有矢量流完全沒有的性質--量子反常。
極矢量和軸矢量的判別
在垂直於所討論的矢量平面內得到該矢量在平面鏡中的像,若該矢量的鏡像和原有矢量的方向相反,則此矢量是極矢量。如質點的位移矢量,在垂直於位移矢量的平面鏡內看到質點的位移方向與原矢量方向相反,故位移矢量是極矢量。同樣可判別力、速度、加速度、動量、衝量、電場強度 等為極矢量。若所討論的矢量的鏡像與原有矢量方向相同,則此矢量是軸矢量。如繞固定軸轉動的剛體的角速度矢量,在垂直於角速度的平面鏡內看到剛體的鏡像,其角速度 仍按原方向旋轉,其矢量的鏡像方向與原矢量方向一致,,故角速度是軸矢量。採用同樣的方法可判別力矩、角動量、角加速度等為軸矢量。
刀軸矢量的控制方式
刀軸矢量的控制方式在多軸數控加工中非常重要,它決定了刀具與被加工表面之間是否產生干涉、相鄰刀軸是否平穩變化、工具機實際加工時能否超程和刀具的有效加工空間等等。對於CAM軟體中提供的各種傾斜方式,必須根據不同的加工特徵合理的進行選擇,才能達到理想的加工效果。常用的幾種傾斜方式有沿切削方向傾斜、過點傾斜、過曲線傾斜,而不傾斜且與曲面垂直這種方式多用於定位加工。通過設定前傾角和側傾角、合理選擇空間點的坐標和曲線的方程可獲得非干涉刀軸矢量,最後利用CAM軟體中自帶的仿真功能進行模擬驗證。

